
4th USENIX Symposium on Networked Systems Design & Implementation
Pp. 313–326 of the Proceedings
Octant: A Comprehensive Framework for the Geolocalization of Internet Hosts
Bernard Wong, Ivan Stoyanov, Emin Gün Sirer
Dept. of Computer Science, Cornell University, Ithaca, NY 14853
|
ABSTRACT
Determining the physical location of Internet hosts is a critical
enabler for many new location-aware services. In this paper, we present Octant,
a novel, comprehensive framework for determining the location of
Internet hosts in the real world based solely on network
measurements. The key insight behind this framework is to pose the geolocalization problem formally
as one of error-minimizing constraint satisfaction, to create a system of
constraints by deriving them aggressively from network measurements, and to
solve the system geometrically to yield the estimated region in which the
target resides. This approach gains its accuracy and precision by taking
advantage of both positive and negative constraints, that is, constraints on
where the node can and cannot be, respectively. The constraints are represented
using regions bounded by Bézier curves, allowing precise
constraint representation and low-cost geometric operations. The framework can
reason in the presence of uncertainty, enabling it to
gracefully cope with aggressively derived constraints that may contain errors.
An evaluation of Octant using PlanetLab nodes and public traceroute servers
shows that Octant can localize the median node to within 22 mi., a factor of three
better than
other evaluated approaches.
1 INTRODUCTION
Determining the physical location of an Internet host is a key enabler for
a wide range of network services. For example, mapping nodes to locations on
the globe enables customized content on the web, simplifies network management
in large installations, and aids network diagnosis. Accurately
determining the position of a node in the real world based solely on network
measurements, however, poses many challenges. The key obstacles to accurate and
precise geolocalization are threefold: how to represent network locations for
nodes, how to extract constraints on where nodes may or may not be located,
and how to combine these constraints to yield good estimates of node
position 1.
In this paper, we present a novel, comprehensive framework for geolocating
Internet hosts called Octant 2. Octant provides an intuitive and generic
framework which represents node positions precisely using regions, expresses
constraints succinctly as areas, and computes positions accurately by solving
a system of geometric constraints. A small number of landmarks whose positions
are approximately known anchors the constraint system to the physical globe.
The Octant approach is comprehensive and general; it
enables almost all past work on geolocalization to be expressed within the
framework, as a (limited) subset of the techniques described in this paper.
Past approaches to geolocalization on the Internet rely solely on positive
information, that is, information on where a node may be located. For
instance, a landmark that pings the target may conclude that the target must
lie within a disk centered around the landmark whose radius is bounded by the
speed of light times the one-way ping latency. In addition to such positive
information, Octant can take advantage of negative information, that is,
information on where the node may not be located. For instance, momentarily
assuming an ideal network with no queuing delays, Octant enables a landmark
that measures a high ping latency to express the fact that the node is at least
a minimum distance away from the landmark.
Octant represents the potential area where a node may be located explicitly as
a surface bounded by Bézier curves. In contrast with past work that keeps track
of and computes a single position estimate, Octant's geolocalization yields a
set of points expressed as an enclosed, potentially non-convex and disconnected
area where the node might lie. The Bézier curve representation enables these
areas to be expressed precisely in a compact manner, and boolean operations on
areas such as union, intersection, and subtraction are computed efficiently.
We outline a Monte Carlo technique for selecting a single, representative point
estimate from such sets to facilitate comparisons with past work and to support
legacy applications which expect a location estimate consisting of a single
point. In practice, Octant's location estimates are accurate, that is, they
almost always contain the actual physical location of the target in the
estimated area, as well as precise, that is, the size of the estimated area is
small.
Since networks rarely follow idealized models of transmission, the fidelity of
geolocation schemes are fundamentally limited by how aggressively they mine the
network for constraints. Given the relatively high variance in the correlation
between network latency and geographical distance due to congestion and
indirect routing, extracting useful positive and negative information is a
challenge. Octant uses various principled methods to extract precise
constraints from noisy Internet measurements. It compensates for dilation
stemming from inelastic delays incurred on the last hop
by computing an extra “height” dimension, that
captures
the effects.
It minimizes
the impact of indirect routes
through piecewise localization of routers on the network path, where it
localizes ordinary routers on the path and uses their approximate location to
further refine the position estimate of the target node. Finally, Octant
uses a weighted solution technique where weights correspond to confidence in a
derived constraint to enable the use of aggressive constraints in addition to
conservative ones without creating a non-solvable constraint system.
The Octant framework is general and comprehensive. Where available,
data from the WHOIS database, the DNS names of routers, and the known locations
of uninhabited regions can be naturally integrated into the solution to refine
it further. Interestingly, this optimization has enabled Octant to identify
“misnamed” routers whose DNS names, based on their ISP's naming convention,
would indicate that they are in a particular state when in reality they are
several hundred miles away (and are named after a node with which they peer).
Overall, this paper presents a geolocalization system for determining the
physical location of hosts on the Internet, and makes three contributions.
First, this paper provides a novel and general framework for expressing
location constraints and solving them geometrically to yield location
estimates. The solution technique, based on Bézier-regions, provides a
general-purpose foundation that accommodates any geographic constraint. Second,
the paper shows how to aggressively extract constraints from network latency
data to yield highly accurate and precise location estimates. Finally, the
paper describes a full implementation of the Octant framework, evaluates it
using measurements from PlanetLab hosts as well as public traceroute servers,
and compares directly to past approaches to geolocalization. We show that the
system achieves a median accuracy of 22 miles for its position estimates.
In contrast, the best accuracy achieved by GeoLim [],
GeoPing [], and GeoTrack []
achieves a median accuracy of 70 miles.
Overall, the system is practical,
provides a location estimate in under a few seconds per target and achieves
high accuracy and precision.
2 RELATED WORK
Past work on geolocalization can be broken down into approaches that
determine a single point estimate for a target, and those that, like Octant,
provides a region encompassing the set of points where the target may lie.
2.1 SINGLE-POINT LOCALIZATION
IP2Geo [] proposes three different techniques for
geolocalization, called GeoPing, GeoTrack and GeoCluster. GeoPing maps the
target node to the landmark node that exhibits the closest latency
characteristics, based on a metric for similarity of network
signatures []. The granularity of GeoPing's geolocalization depends
on the number and location of the landmarks, requiring a landmark to be close
to each target to produce low-error geolocation.
GeoTrack performs a traceroute to a given target, extracts
geographical information from the DNS names of routers on the path,
and localizes the node to the last router on the path whose position
is known. The accuracy of GeoTrack is thus highly
dependent on the distance between last recognizable router
to the landmark, as well as the accuracy of the positions extracted
from router names.
GeoCluster is a database based technique that first breaks the IP
address space into clusters that are likely to be geographically co-located,
and then assigns a geographical location to each cluster based on
IP-to-location mappings from third party databases. These databases include
the user registration records from a large web-based e-mail service,
a business web-hosting company, as well as the zip-codes of users of
an online TV program guide. This technique requires a large,
fine-grain and fresh database. Such databases are not readily
available to the public due to potential privacy concerns, the
clustering may not sufficiently capture locality, the accuracy of such
databases must be perpetually refreshed, and, most importantly, the
overall scheme is at the mercy of the geographic clustering performed
by ISPs when assigning IP address ranges.
Services such as NetGeo [] and IP2LL [] geolocalize an
IP address using the locations recorded in the WHOIS database for the
corresponding IP address block. The granularity of such a scheme is very
coarse for large IP address blocks that may contain geographically diverse
nodes. The information in the WHOIS database is also not closely regulated and
the address information often indicates the location of the head office of
the owner which need not be geographically close to the actual target.
Quova [] is a commercial service that provides IP geolocalization
based on its own proprietary technique. Neither the details of the technique
nor a sample dataset are publicly available.
There are several graphical traceroute tools that offer the geographical
location of each intermediate router. GTrace [] successively
uses DNS LOC entries, a proprietary database of domain name to geographical
location mappings, NetGeo, and domain name country codes, as available, to
localize a given node. VisualRoute [] is a commercial
traceroute tools that also offer geographic localization of the nodes along the
path.
2.2 REGION LOCALIZATION
GeoLim [] derives the estimated position of a node by measuring the
network latency to the target from a set of landmarks, extracts upper bounds on
position based on inter-landmark distance to latency ratios, and locates the
node in the region formed by the intersection of these fixes to established
landmarks. Since it does not use negative information, permit non-convex
regions or handle uncertainty, this approach breaks down as inter-landmark
distances increase.
In contrast, Octant provides a general framework for combining both positive
and negative constraints to yield a small, bounded region in which a node is
located. It differs from past work in that it enables negative information
to be used for localization, separates the selection of a representative
point estimate from the computation of the feasible set of points in which a
node might be located, permits non-convex solution areas, and aggressively
harvests constraints from network latency measurements.
Topology-based Geolocation (TBG) [] uses the maximum transmission speed
of packets in fiber to conservatively determine the convex region where the
target lies from network latencies between the landmarks and the target.
It additionally uses inter-router latencies on the landmarks to target
network paths to find a physical placement of the routers and target that
minimizes inconsistencies with the network latencies. TBG
relies on a global optimization that minimizes average position error for
the routers and target. This process can introduce error in the target
position in an effort to reduce errors on the location of the intermediate
routers. Octant differs from TBG by providing a geometric solution technique
rather than one based on global optimization. This enables Octant to
perform geolocalization in near real-time, where TBG requires significantly
more computational time and resources. A geometric solution technique also
allows Octant to seamlessly incorporate exogenous geometric constraints
stemming from, for example, geography and demographics. This provides Octant
with more sources of information for its geolocalization compared to TBG.
Localization has been studied extensively in wireless systems. The wireless
localization problem, however, is significantly different from, and easier
than, localization on the Internet, as air is close to a perfect medium with
well-understood transmission characteristics. The most comprehensive work on
localization in wireless networks is Sextant []. We share with
Sextant the basic insight for accommodating both positive and negative
constraints and enabling constraints to be used by landmarks whose positions
are not known definitively. Octant differs substantially from Sextant in
the various mechanisms it uses to translate Internet measurements to
constraints, including its mapping of latencies to constraints, isolating
last hop delays, and compensating for indirect routes, among others.
3 FRAMEWORK
The goal of the Octant framework is to compute a region βi that
comprises the set of points on the surface of the globe where node i
might be located. This estimated location region βi is
computed based on constraints γ0 … γn provided to
Octant.

Figure 1: Location representation in Octant. Octant represents
the estimated target location as a region bounded by a set
of Bézier curves.
Each curve a, b, c consists of four control points
P0, ..., P3 with
P0 and P3 as the start and end points respectively and
P1 and P2 as control points that help direct the curve.
This figure requires a total of only nine control points to precisely
define. Bézier curves provide a compact way to represent large,
complex areas precisely. They also admit efficient intersection,
union, and subtraction operations.
A constraint γ is a region on the globe in which the target
node is believed to reside, along with an associated weight that
captures the strength of that belief. The constraint region can have
an arbitrary boundary, as in the case of zipcode information extracted
from the WHOIS database or coastline information from a geographic
database. Octant represents such areas using Bézier-regions, which
consist of adjoining piecewise Bézier curves as illustrated in
Figure 1. Bézier curves are
polynomial parametric curves with n+1 control points P0, ..., Pn
where n is the order of the polynomial, with n=3 for most
implementations. Intuitively, the points P0 and Pn are the start
and end points with the remaining points providing the directional
information. Bézier regions provide both precise and compact
representation of complex shapes. For example, a circle can be
represented exactly using four adjoining Bézier curves and a total of
twelve control points.

Figure 2: Octant computes an estimated location region for a target node
by combining positive and negative information available through latency measurements. The resulting
location estimate comprises non-convex, potentially disjoint regions separated by weight.

Figure 3: Comprehensive use of positive and negative
constraints in Octant. (a) A primary landmark, with a precise position
estimate, and its associated constraints.
(b) Positive constraints are calculated by taking the union of all circles in
the estimated area. A node within distance d must reside in the region marked
with the dark outer line. Only a subsample of the circles are shown for clarity.
(c) Negative constraints are computed by taking the intersection of all circles
in the estimated area. A node outside of distance d can not be in the region
marked with the dotted line.
(d) A secondary landmark, whose position is not known precisely. Note that the
associated constraints lead to a larger annulus, due to the conservative, sound
way in which Octant combines them. An implementation may replace complex Bézier
regions with a bounding circle for efficiency.
Typically constraints are obtained via network measurements from
a set of nodes, called landmarks, whose physical locations are
at least partially known. Every landmark node Lj has an associated
estimated location region βLj, whose size captures the
amount of error in the position estimate for the landmark. We call a
node a primary landmark if its position estimate was created via
some exogenous mechanism, such as a GPS measurement or by mapping a
street address to global coordinates. Typically, primary landmarks
have very low error associated with their position estimates. We call
a node a secondary landmark if its position estimate was
computed by Octant itself. In such cases, βLj is the result
of executing Octant with the secondary landmark Lj as the target
node.
Octant enables landmarks to introduce constraints about the location
of a target node based either on positive or negative
information. A positive constraint is of the form “node A
is within x miles of Landmark L1,” whereas a negative constraint
is a statement of the form “node A is further than y miles from
Landmark L1.” On a finite surface, such as the globe, these two
statements both lead to a finite region in which the node is believed
to lie. However, the nature of the constraint, either positive or
negative, makes a big difference in how these regions are computed.
In the simple case where the location of a primary landmark is known
with pinpoint accuracy, a positive constraint with distance d
defines a disk with radius d centered around the landmark in which
the node must reside. A negative constraint with distance d' defines
the complement, namely, all points on the globe that are not within
the disk with radius d'. In typical Octant operation, each landmark
Lj contributes both a positive and a negative constraint. When the
source landmark is a primary whose position is known accurately, such
constraints define an annulus.
Octant enables meaningful extraction of constraint regions even when the
position of the landmark is approximate and consists of an irregular region.
For a secondary landmark k whose position estimate is βk, a positive
constraint with distance d defines a region that consists of the
union of all circles of radius d at all points inside βk
(formally, γ = ∪(x.y)∈βk c(x,y,d) where
c(x,y,d) is the disk with radius d centered at (x,y)). In
contrast, a negative constraint rules out the possibility that the
target is located at those points that are within distance d
regardless of where the landmark might be within βk (formally,
γ = ∩(x,y)∈βk c(x,y,d)).
Given the description above, it may seem that computing these intersection
and union regions might take time proportional to the area of βk,
and thus be infeasible. Octant's representation of regions using
Bézier curves enables these operations to be performed very
efficiently via transformations only on the endpoints of Bézier
segments. Since Bézier curves are used heavily in computer graphics,
efficient implementations of Bézier clipping and union operations are
available. However, the number of Bézier segments in a region
increases with each intersection and union operation, which gradually
expands the number of curves to track and manipulate, which in turn
poses a limit to the scalability of the framework. So a scalable
Octant implementation may decide to approximate certain complex
βk with a simple bounding circle in order to keep the number of
curves per region in check and thus gain scalability at the cost of
modest error. Figure 3 illustrates the derivation of
positive and negative constraints from primary and secondary
landmarks.
Given a set Ω of positive constraints and a set Φ of
negative constraints on the position of a target node i, the estimated
location region for the target is given by:
βi = ∩Xi ∈ Ω Xi \ ∪Xi ∈
Φ Xi.
This equation is precise and lends itself to an efficient and elegant
geometric solution. Figure 2 illustrates how Octant combines
constraints to yield an accurate estimated location region for a
target.
There are, however, many issues to solve before this approach can be
used for practical geolocalization on the Internet. In the general
formulation above, all constraints are weighted equally and the
solution is discrete; a point is either part of the solution space or
it is not. A discrete solution strategy leads to a brittle system, as
a single erroneous constraint will collapse the estimated location
region down to the empty set. One strategy is to use only highly
conservative positive constraints derived from the speed of light
and avoid all negative constraints. We show later that such a
conservative strategy does not achieve good precision. In the next
set of sections, we detail optimizations that enable the basic Octant
framework to be applied to noisy and conflicting measurements on the
Internet.
If latencies on the Internet were directly proportional to distances
in the real world, the geolocalization problem would be greatly
simplified. Three factors complicate Internet
latency measurements. First, the Internet consists of heterogeneous
links, hosts and routers whose transmission and processing speeds vary
widely. Second, inelastic delays incurred on the last hop can
introduce additional latencies that break the correspondence between
round trip timings and physical distances. Finally, packets often
follow indirect, circuitous paths from a source to a destination,
rendering great-circle approximations inaccurate. In the next three
sections, we address each of these problems in turn.
3.1 MAPPING LATENCIES TO DISTANCES
The network latency between a target and a landmark physically bounds their
maximum geographical distance. A round-trip latency measurement of d
milliseconds between a landmark and a target can be translated into a
distance constraint using the propagation delay of light in fiber,
approximately 2/3 the speed of light. This yields a
conservative positive constraint on node locations that can then be
solved using the Octant framework to yield a sound estimated position for
the target; such an estimate will never yield an infeasible (∅)
solution. In practice, however, such constraints are so loose that they
lead to very low precision.

Figure 4: The latency-to-distance plot of peer landmarks for
a representative landmark (planetlab1.cs.rochester.edu). The shaded region
denotes the valid point locations as bounded by the propagation delay time of
light in fiber. The convex hull around the data-points serves as the positive
and negative constraints for the node. For a given latency, the top and
bottom of the hull represent the outer and inner radius respectively of the
constraint annulus. As distances increase, fewer representative nodes remain,
rendering the convex hull overly aggressive. Vertical lines indicate the 50 and
75th percentile cutoffs, where the convex hull is cut and replaced with
conservative positive and negative constraints when insufficient representative
nodes remain.
Yet the correlation between latency measurements and real-world distances is
typically better and tighter than constraints based on the speed of light.
Figure 4 plots the network latency against physical
distance from a primary landmark (planetlab1.cs.rochester.edu) to all other
primary landmarks in our study. The figure makes clear the loose correlation
between physical distance and illustrates how overly conservative the speed of
light bounds can be. In addition, the empty region to the lower right suggests
that few links are significantly congested; nodes that are physically close are
typically reachable in a short amount of time. This presents an opportunity for
a system wishing to aggressively extract constraints at the risk of
occasionally making overly aggressive claims, to both tighten the bounds on
positive constraints and to introduce negative constraints.
Octant calibrates each landmark when the landmark is initialized as
well as periodically to determine the correlation between network
measurements performed from that landmark and real-world distances.
The goal of the calibration step is to compute two bounds RL(d) and
rL(d) for each landmark L and latency measurement d such that a
node i whose ping time is d will be between
rL(d) ≤ || loc(L) − loc(i) || ≤ RL(d). This permits Octant to
extract a positive and a negative constraint for each
measurement made from each landmark. Note that when rL(d) = 0, the negative
constraint is defunct and does not play a role in localization; for nodes that
are so close that ping times are dominated by queuing delays, rL should be zero.
A principled approach is used to conservatively pick RL and rL.
Each landmark periodically pings all other landmarks in the system, creating a
correlation table much like Figure 4. It then determines
the convex hull around the points on the graph. Functions RL and rL
correspond to the upper and lower facets of the convex hull. This approach for
extracting constraints is both tight and conservative. The RL and rL
bounds do not contradict any empirical results, as the convex hull envelopes all
data points measured at the landmark. The bounds are significantly tighter
than bounds derived from linear functions used in previous
techniques []. And the convex hull facets are smooth, positively
sloped, and closely track the average latency to distance correlation.
In practice, this approach yields good results when there are sufficient
landmarks that inter-landmark measurements approximate landmark-to-target
measurements.
In cases where the target has a direct and congestion-free path to the
landmark, it may lie beyond RL(d), and vice versa for rL(d).
While extensions to Octant we discuss later can compensate for occasional
errors, the r and R estimates may be systematically wrong when there are
just insufficient landmarks to draw statistically valid conclusions.
Consequently, Octant introduces a cutoff at latency ρ, such that a
tunable percentile of landmarks lie to the left of ρ, and discards the
part of the convex hull that lies to the right of ρ. That is, only the
part of the convex hull for which sufficient data points are available is
taken into consideration. Octant then uses
rL(x) = rL(ρ), ∀ x ≥ ρ, and
RL(x) = m (x − ρ) + RL(ρ), m = (yz − RL(ρ)) / (xz − ρ),
where a fictitious sentinel datapoint z, placed far away, provides a
smooth transition from the aggressive estimates on the convex hull towards
the conservative constraints based on the limits imposed by the speed of light.
3.2 LAST HOP DELAYS
Mapping latencies to distances is further complicated by additional queuing,
processing, and transmission delays associated with the last hop. For home
users, these last hop delays can be attributed to cable and DSL connections
that are often under-provisioned.
Even in the wide area, the processing overhead on servers adds additional
time to latency measurements that can overshadow the transmission
delays. For instance, on overloaded Planetlab nodes, measured latencies can
be significantly inflated even with careful use of kernel timestamps.
Consequently, achieving more accurate and robust localization results
requires that we isolate the inelastic delay components which
artificially inflate latency measurements and confound the latency
to distance correlation.
Ideally, a geolocalization system would query all routers on all
inter-node paths, isolate routers that are present on every path from each node, and
associate the queuing and transmission delays of these routers along with the node's
average processing delay as the inelastic component of the node. Since
this approach is impractical, we need a feasible way to approximate
the last hop delay from latency measurements.
Three properties of the problem domain motivate an end-to-end approach to the
measurement and representation of last hop delay in Octant. First, localization
needs to be performed quickly without the cooperation of the target host.
This rules out the use of precise timing hardware for packet dilation, as well
as software approaches that require pre-installed processing code on the target.
Second, creating detailed maps of the underlying physical network, as in
network tomography [, ], entails significant
overhead and does not yet provide answers on the timescales necessary for
on-the-fly localization. Third, Octant has mechanisms in place to accommodate
uncertainty in constraints (section 3.4) and can thus afford
imprecision in its last hop delay estimates.
These properties led us to use a fast, low-overhead, end-to-end approach for
capturing the last hop delay seen on measurements from a given host in
a single, simple metric which we call height.
Octant derives height estimates from pair-wise
latency measurements between landmarks. Primary landmarks, say a, b,
c, measure their latencies, denoted [a,b], [a,c], [b,c].
The measure for latency is the round-trip time, which captures the
last hop delays in both link directions. Since the
positions of primary landmarks are known, the great circle distances
between the landmarks can be computed, which yield corresponding
estimates of transmission delay, denoted (a,b), (a,c), (b,c). This
provides an estimate of the inelastic delay component between any two
landmarks 3;
for instance, the inelastic delay component between landmarks a and b is [a,b]
− (a,b). Octant determines how
much of the delays can be attributed to each landmark, denoted a',
b', c', by solving the following set of equations:
⎡
⎢
⎢
⎣ |
|
⎤
⎥
⎥
⎦ |
|
⎡
⎢
⎢
⎣ |
|
⎤
⎥
⎥
⎦ |
|
= |
⎡
⎢
⎢
⎣ |
| [a,b] − (a,b) |
| [a,c] − (a,c) |
| [b,c] − (b,c) |
|
⎤
⎥
⎥
⎦ |
|
Similarly, for a target t, Octant can compute t',as well as an
estimate of the longitude and latitude, tlong and tlat,
by solving the following system of equations:
| a' + t' + (a,t) |
= |
[a,t] |
| b' + t' + (b,t) |
= |
[b,t] |
| c' + t' + (c,t) |
= |
[c,t] |
where (a,t) can be computed in terms of along, alat,
tlong, tlat. We can then solve for the t', tlong, tlat
that minimizes the residue. The computed tlong and tlat result,
similar to the synthetic coordinates assigned by [], has relatively high
error and is not used in the later stages. The target node itself
need not participate in the solution for its height, except by responding to
pings from landmarks. Figure 5 shows the heights of
the landmarks in our PlanetLab dataset.
Given the target and landmarks' heights, each landmark can shift its RL
up if the target's height is less than the heights of the other landmarks,
and similarly shift its rL down if the target's height is greater than the
heights of the other landmarks.
This provides a principled basis for ensuring that at least a fraction of the
time packets spend in the last hop do not skew the derived constraints.

Figure 5: Heights computed by Octant to capture last hop delays on
network paths to geographically distributed landmarks. Vertical bars
represent landmarks, their position corresponds to their physical
location, while the length of the bars corresponds to their assigned
heights.
3.3 INDIRECT ROUTES
The preceding discussion made the simplifying assumption that route
lengths between landmarks and the target are proportional to great
circle distances. Studies [] have shown that this is often
not the case in practice, due to policy routing. For instance, routes
between subscribers in Ithaca, NY and Cornell University traverse
Syracuse, NY, Brockport, IL, and New York City before getting routed
back to Cornell, traveling approximately 800 miles to cover less than
a mile of physical distance. A geolocalization system with a built-in
assumption of proportionality would not be able to achieve good
accuracy.
Note that the preceding section on height computation addresses
some, but not all, of the inaccuracies stemming from indirect
routes. In the example above, if all packets from this landmark get
routed through Syracuse, NY, the distance between Ithaca and Syracuse will
be folded into the landmark's height, enabling the landmark to
accurately compute negative information even for nodes that are near
it (without the height, the landmark might preclude its next door
neighbors from being located in Ithaca). The height optimization,
however, does not address inaccuracies stemming from the inconsistent,
or unexpected use of indirect routes. Specifically, nodes with
otherwise low heights might choose unexpectedly long and circuitous
routes for certain targets. This occurs often enough in practice that
accurate geolocalization requires a mechanism to compensate for its
effects.
Octant addresses indirect routes by performing piecewise localization, that is
localizing routers on the network path from the landmarks to the target
serially, using routers localized on previous steps as secondary
landmarks. This approach yields much better results than using just end-to-end
latencies, and is illustrated in Figure 6. Since
Octant can perform localization based solely on round-trip timings, localizing
routers does not require any additional code to be deployed.
While the Octant framework can be used as is to locate routers, the
structured way in which most routers are named enables Octant to
extract more precise information about their location. Octant performs
a reverse DNS lookup on each router on the path and determines the
city in which it resides by using the undns [] tool,
which extracts locations from ISP-specific naming patterns in router
names. The city names for routers with city information are converted into
geographical coordinates using data from the US census zipcode database.
A given city can have multiple coordinates in the database, with each
representing the location of a zipcode region. The location of a router of a
given city is the bounding circle encompassing the city's coordinates with a
tunable slack to account for large zipcode regions. This approach yields much
better results than using just end-to-end latencies, as routes between routers
separated by a single link is largely void of indirect routing.

Figure 6: The use of intermediate routers as secondary landmarks can
significantly increase localization accuracy. Octant is used first
to determine the estimated location area for a router. Where
possible, Octant refines location estimates based on the city,
extracted from the router's DNS name with undns, in which the
router is located. This is shown for Indianapolis
and Houston, where dots represent the center of every zipcode located in
that city. For Buffalo and Kansas City, the location of the
routers is computed using Octant without undns information.
The rings around Buffalo and Ithaca are omitted for clarity.
3.4 HANDLING UNCERTAINTY
A mechanism to handle and filter out erroneous constraints is critical to
maintaining high localization accuracy. The core mechanism Octant uses is to
assign weights to constraints based on their inherent accuracy.
For latency-based constraints, we have observed that the accuracy of
constraints from landmarks that have high latency to the target are less
trustworthy than those that are nearby. The simple intuition behind this is
that the increase in latency is either due to far-away nodes that have a higher
probability of traversing through indirect, meandering routes or travel along
paths that have high congestion, which often results in constraints that are of
relatively little use compared to nearby nodes.
Octant uses a weight system that decreases exponentially with
increasing latency, thereby mitigating the effect of high-latency
landmarks when lower latency landmarks are present. A weight is associated
with each constraint based on the latency between the originating landmark and
the target node. When two regions overlap, the weights are added
together. In the absence of weights, regions can be combined via union
and intersection operations, leading to a discrete solution for a
location estimate - the node is either within a region, or lies
outside. The introduction of weights changes the implementation. When
two regions overlap, Octant determines all possible resulting regions
via intersections, and assigns the associated weight to each. The
final estimated location region is computed by taking the union of all
regions, sorted by weight, such that they exceed a desired weight or region
size threshold.
Weights enable Octant to integrate constraints of questionable verity
into the system. Recall that, when the resulting area is the empty
set, going back and finding the minimal set of constraints that led to
an infeasible solution is an NP-complete problem. Weights allow
conflicting information to be introduced into the system at little
risk of over-constraining the final system and reducing its
effectiveness; overaggressive constraints from latency measurements,
incorrect zipcode from WHOIS, or misnamed routers in undns will not
just render the solution down to the empty set. Bad constraints
may still impact accuracy if there are no compensating factors,
but weights enable Octant to associate a probability measure
with regions of space in which a node might lie.
3.5 ITERATIVE REFINEMENT
Localization in the Octant framework can be broken down into two phases.
The first is to use accurate and mostly conservative constraints to construct
an estimated location region that contains the target with high
probability. A second optional phase is to use less accurate and more
aggressive constraints to obtain a better estimate of the target
location inside the initial estimated region.
In section 3.1, we introduced a scheme by which
tight bounds can be established for the negative and positive
constraints. While that approach, based on computing the convex hull that includes all
inter-landmark measurements, achieves high accuracy in practice, it may sometimes return
estimated location regions that are too big and imprecise. The reader
will observe that it may be possible to use even more aggressive
constraints than those dictated by the discussion so far and achieve
smaller estimated location regions. The downside of more aggressive
constraints is that they may yield an infeasible system of
constraints, where the estimated region collapses down to the empty
set. In between these two extremes is a setting at which constraints
are set just so that the feasible solution space is below a desired
parameter. Iterative refinement is an extension to the basic Octant
framework to find this setting.
During the calibration phase, Octant additionally computes for each
landmark the interpolated spline that minimizes the square error to the
latency-to-distance data-points of its inter-landmark measurements, as
shown with the dashed lines in Figure 4. Opportunistic positive
constraints are then derived from the spline by multiplying the spline
by a constant δ, while negative constraints are computed by
dividing the spline by δ. The value of δ is chosen such
that the upper and lower bound contains a given percent of the total number of
data points.
Octant initially uses the constraints obtained from the convex hull to
compute, typically, a relatively large estimated location area. It
then uses this area as a clipping region, which enables it to run
through subsequent iterations very quickly, as it can discard all
regions that lie outside the initial solution space. The iterative
refinement stage then steps through values for δ, recomputing
the estimated location area with successively tighter constraints. The
process can terminate when the solution space is below a targeted
area, is empty, or when a timeout is reached. This optimization enables
Octant to determine how aggressively to extract constraints from the
network automatically, without hand tuning.
3.6 GEOGRAPHICAL CONSTRAINTS

Figure 7: Using the city constraints to localize the
planetlab2.flux.utah.edu target can significantly reduce the
estimated region size as the gaps between the cities can
be removed.
In addition to constraints extracted from latency measurements, Octant
enables any kind of geographical constraint, expressed as arbitrary
Bézier-regions, to be integrated into the localization process. In
particular, Octant makes it possible to introduce both positive (such
as zipcodes from the WHOIS database, zipcodes obtained from other
users in the same IP prefix []) and negative
constraints (such as oceans, deserts, uninhabitable areas) stemming
from geography and demographics. Clipping estimated location regions
with geographic constraints can significantly improve localization
accuracy. Since it is highly unlikely for the system to have landmarks
in such areas, negative information is typically not available to rule
them out. As a result, estimated regions can extend into oceans. In
prior work, which does not permit non-convex regions, the removal of such
areas typically requires an ad hoc post-processing step. In contrast,
Octant can naturally accommodate such constraints during its
estimation process. The application of geographic data, such as ocean
boundaries, and demographic data, such as population density maps, can
vastly improve precision. Figure 7 shows the
city constraints for a target node in Utah, which is otherwise quite
difficult to localize precisely due to its distance to all other
landmarks and terrain features.
3.7 POINT SELECTION
The Octant approach to localization computes a final estimated localization region
which captures the system's best estimate of where the target must lie. Some applications
can use such area estimates directly. For instance, web applications might generate
content, such as real estate listings, based on the potential zipcodes in which the viewer may be located.
Octant can provide the area as either Bézier curve bounded surfaces or an ordered
list of coordinates to these applications.
Yet many legacy applications, as well as past work, such as GeoPing and GeoTrack,
localize targets to a single point.
In order to support legacy applications and provide a comparison to previous work, Octant uses a
Monte-Carlo algorithm to pick a single point that represents the best estimate of the target's location.
The system initially selects thousands of random points that lie within the
estimated region. Each point is assigned a weight based on the sum of
its distances to the other selected points. After some number of trials,
the point with the least weight is chosen as the best estimate of the
target's location. This point is guaranteed to be within the estimated location area
by definition, even if the area consists of disjoint regions.
Ideally, Octant's point selection interface would only serve in a
transitional role for legacy application support.
We hope that future applications will be made general enough to take advantage
of the extra information in Octant's estimated area.

Figure 8: Comparison of the accuracy of different localization
techniques in the PlanetLab dataset. Octant achieves
significantly greater accuracy than previous work, yielding
point estimates for nodes that are substantially closer to
the real positions of the targets.
4 IMPLEMENTATION
The Octant framework for geolocalization is practical, entails low
measurement overhead and is computationally inexpensive to execute. The core
operations involve the manipulation of Bézier curves, which is
a compact representation of curves specified by four control points. Standard
libraries support common operations, such as intersection, subtraction, and
union on Bézier curves, and implement them efficiently by manipulating
only the control points []. In addition, Bézier curves are
robust to slight inaccuracies in their control points [].
Our Octant implementation does not depend on having control of the target node,
or the intermediate routers between the landmarks and the target.
Ideally, the target should respond to probes consistently and quickly. A target
behind a slow last mile link, or a slow target that incurs high interrupt and processing latencies for all responses
will have its response latency factored into its height, which will then compensate for the
node's slower speed. Targets that are inconsistent can pose problems; our current implementation
performs 10 ICMP pings and uses the minimum RTT time as the basis for extracted constraints.
Overall, the code consists of 9800 lines of code, whose structure enables it to operate as a
third party service, providing geolocalization results given an IP address using only about 50
nodes deployed on the Internet. When a new landmark comes online, it goes through the
calibration phase, measures its latencies to other landmarks, and ships its results
back to a centralized server. From then on, the landmarks
simply perform ping measurements to target IP addresses and report their results to the centralized server. The server
performs the localization by combining the constraints. On a 2GHz machine, this operation currently takes a few seconds once the
landmarks are calibrated. The system can easily be made decentralized or optimized further, though our focus has been
on improving its accuracy rather than its speed, which we find reasonable.
5 EVALUATION

Figure 9: The percentage of targets inside the Octant's location
estimate is significantly higher than GeoLim's due to
Octant's mechanisms for handling uncertainty of individual
landmark's location estimate.
We evaluated Octant using physical latency data collected from a
PlanetLab dataset consisting of 51 PlanetLab [] landmark nodes
in North America, as well as a public traceroute server dataset consisting
of 53 traceroute servers maintained by various commercial and academic
institutions in North America. The latency data for the PlanetLab dataset and the
public traceroute servers dataset were collected on Feb 1, 2006 and
Sept 18, 2006, respectively, using 10 time-dispersed ICMP ping probes to measure
round-trip times. Kernel timestamps were used in the latency measurements to
minimize timing errors due to overloaded PlanetLab nodes. To evaluate the
efficacy of using secondary landmarks, we also collected the full traceroute
information between every landmark and target pair, as well as latency data
between the landmarks and intermediate routers. Whenever appropriate, we repeat
measurements 10 times, randomizing landmark selection, and plot the
standard deviation.
Evaluating the accuracy of a geolocalization system is difficult,
because it necessitates a reliable source of IP to location mappings
that can be used as the “ground truth.” Such an authoritative mapping is
surprisingly difficult to obtain. Our evaluation relies on a total of
104 targets, chosen from the PlanetLab and the traceroute server
datasets as described below. We limit our study to North America as
the number of PlanetLab nodes on other continents is too few to yield
statistically significant results. We vary the number of landmarks inside North
America to examine the behavior of the system at lower densities.
In our PlanetLab dataset, nodes serve both as landmarks and targets,
following [, ]; of course, the node's own
position information is not utilized when it is serving as a target. No two
hosts in our evaluation reside in the same institution, which rules out simple
yet unrealistic and unscalable solutions to geolocalization that rely on
having a nearby landmark for every target.
The traceroute servers in the public traceroute server dataset are
used only as targets, with 32 PlanetLab nodes serving as landmarks. The
individual traceroute server owners specify the location of their traceroute
servers as part of the traceroute service. However, these
self-provided locations are often erroneous; we eliminate nodes whose
reported positions violate speed of light constraints or disagree with
a commercial IP geolocation database [] from consideration.

Figure 10: The area of Octant's location estimate
is significantly smaller than GeoLim's across all tested number of landmarks.
We first compare Octant with GeoLim, GeoPing, and GeoTrack
on the PlanetLab dataset.
We evaluate these approaches based on their accuracy and precision, and examine
how these two metrics vary as a function of the number of landmarks and
average inter-landmark distance. We examine accuracy in terms of two
metrics: one is the distance between the single point estimate
returned by these geolocalization techniques and the physical location
of the node, while the other is the percent of nodes whose real-world
locations reside within the estimated location area. The former metric
allows us to compare Octant to previous systems, such as GeoPing and
GeoTrack, that compute only a point estimate, and evaluates how well
these systems perform for legacy applications that rely on a single
point position. The latter, applicable only to recent geolocalization
systems including Octant and GeoLim and proposed by
GeoLim [], evaluates how well area-based
approaches perform. Note that comparisons using the latter metric need
to be accompanied by measurements on the size of the estimated area
(otherwise a simple solution containing the globe will always locate
the node accurately), which we also provide.
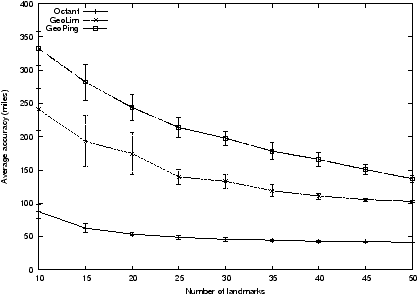
Figure 11: The average distance between a target's physical location
and the single point estimate returned for that target. Octant
achieves high accuracy with low numbers of landmarks.
Figure 8 shows the accuracy of different
geolocalization techniques by plotting the CDF of the distance between the
position estimate and the physical location of a node. Octant
significantly outperforms the other three techniques across the entire set
of targets. The median accuracy of Octant is 22 miles, compared to median accuracy of 89
miles for GeoLim, 68 miles for GeoPing and 97 miles for GeoTrack. GeoLim was not
able to localize approximately 30% of the targets, as its
overaggressive constraint extraction leads to empty regions. Even the
worst case under Octant is significantly lower than the worst cases
encountered with other techniques. The worst case under Octant, GeoLim, GeoPing
and GeoTrack are 173, 385, 1071, and 2709 miles, respectively.
A median error of 22 miles is difficult to achieve based solely on
constraints obtained online from uncoordinated and unsynchronized
hosts, in the presence of routing anomalies and non-great circle
routes. As a point of comparison, if all hosts on the Internet were
connected via point-to-point fiber links that followed great-circle
paths, host clocks were synchronized, and there were no routing
anomalies, achieving such error bounds using packet timings would
require timing accuracy that could accurately distinguish a delay of
22*1.6 / (2/3 * 300000) = 170 microseconds.

Figure 12: The contributions of individual optimizations used in Octant
to geolocalization accuracy. The use of intermediate nodes provides
the largest improvement to system accuracy.
In a typical deployment, the number of landmarks used to localize
a target is often constrained by physical availability, and an
implementation may not be able to use all landmarks in the
localization of all targets due to load limits, node failures, or
other network management constraints.
We evaluate Octant's performance as a function of the number of
landmarks used to localize targets, and compare to GeoLim, the only
other region-based geolocalization system.
Figure 9 shows the number of nodes that
were located successfully; that is, their physical locations were
inside the estimated location region returned by Octant. Three
findings emerge from the plot. First, the percentage of nodes that are
successfully localized is quite high for Octant, averaging more than
90% when the number of landmarks exceeds 15. Second, the accuracy of
the Octant approach remains flat or improves slightly with increasing
numbers of landmarks. Using 15 landmarks yields results that are
almost as good as using all 50, and adding more landmarks does not
hurt performance. Finally, the accuracy of the
GeoLim approach is high for low numbers of landmarks, and drops as
more landmarks are introduced. This surprising behavior is due to
overaggressive extraction of constraints in GeoLim; as the number of
landmarks increases, the chances that a “bad” node, whose network
connection yields an unexpected delay, will introduce an
over-constraint grows. When there are too many conflicting constraints,
GeoLim yields the empty set as its location estimate, whereas
the weighted combination of
constraints enables Octant to avoid these pitfalls. With all 50
landmarks, GeoLim returns the empty set for more than 29% of the
targets.
The preceding evaluation, which examined the percentage of nodes whose
physical locations lie inside their estimated location region, needs
to be coupled with an examination of the size of the estimated
location regions to put the accuracy of the systems in context.
Figure 10 shows the area of the
estimated location region for GeoLim and Octant. The size of the
geolocalization region is quite small for Octant at 10 landmarks, and
remains the same or slowly decreases with additional landmarks. For
small numbers of landmarks, GeoLim returns substantially larger areas
that are a factor of 6 bigger than Octant's, which explains its
ability to localize about 80% of the nodes with 10 landmarks.
Adding more landmarks refines GeoLim's location estimates, though even at
50 landmarks, GeoLim's location estimates are twice the size of Octant's.
Octant is able to keep the region small via its careful extraction of
constraints and use of negative information.

Figure 13: The percentage of targets located on average within their estimated
location areas for Octant, Octant without various optimizations, and GeoLim.
We next examine the absolute error in legacy position estimates based
on a single point. Figure 11 plots the average
distance between a target's physical location and the single point
estimate returned for that target. Octant consistently achieves high
accuracy, even with landmarks as few as 15. In contrast, GeoLim and
GeoPing exhibit performance that degrades as the number of landmarks
decreases and their distribution throughout the space becomes more
sparse. Octant's performance as the number of landmarks decreases
mostly stems from its ability to use routers inside the network as
secondary landmarks. Octant's average error is significantly less
than both GeoPing and GeoLim even when Octant uses a fifth of the
landmarks as the other schemes.
To provide insight into Octant's accuracy, we examine its performance as
we disable various optimizations.
We examine the individual contribution of each of our optimizations, namely
heights, weights, exponential weights and intermediate nodes, by turning
off each one in turn and comparing their accuracy with that of the
complete Octant system. Figure 12 shows the
resulting CDFs.
The largest improvement to system accuracy is due to
the use of intermediate nodes, which significantly increases the
number of usable landmarks in the system. Undns is useful
approximately half the time, but transitive localization is
critical to precise localization.

Figure 14: The area of the location estimate for Octant with demographic and
geographic constraints. The use of these exogenous constraints substantially
reduce the size of the estimated area.
Figures 13 and 14 provide
further insight into the impact of various optimizations on Octant's
accuracy and precision. Figure 13 plots the
percentage of nodes localized with each of the optimizations turned
off. NoInter refers to Octant with localization through secondary
landmarks inside the network turned off, NoWeights uses no weights
associated with constraints, NoHeight disables the last hop delay
approximation, NoExpWeights uses weights but all constraints carry
equal weights. The distinction between NoWeights and NoExpWeights
is subtle but important. In NoWeights, the estimated location of
the target is the intersection of all available constraints.
In contrast, NoExpWeights estimates the location of the target
as the union of all regions above a certain weight threshold. The
effects of a limited number of incorrect constraints can be
mitigated by trading off precision, as chosen by the threshold value.
The largest contribution in improving accuracy,
approximately 33%, stems from the use of weights. GeoLim is less
accurate than all the different Octant configurations, even though its
location estimates are significantly larger.
The use of geographical constraints in Octant significantly reduces the
size of the location estimates. Figure 14
shows the size of the location estimates in square miles for Octant
with the population density (“cities”) constraint which introduces
clipping areas into location estimates weighted by the density of the
population inside that region, with the oceans constraint which clips
oceans from the solution space, and without any
geographic constraints, as well as the location estimate area for
GeoLim. The use of either geographical constraint alone makes a
significant improvement in the location estimate, improving the
precision of the estimates. Combined, these geographical estimates
greatly improve the fidelity of the location estimates returned by
Octant.
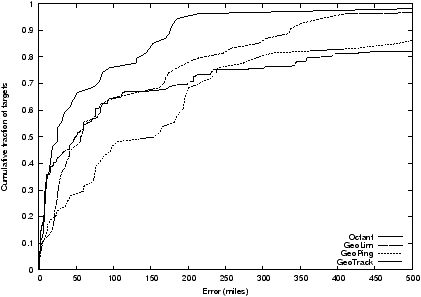
Figure 15: The accuracy of different localization techniques
on the public traceroute servers dataset show very similar
results to those from the PlanetLab dataset, with
Octant yielding point estimates that are significant closer
to the real positions of the targets.
The results from our public traceroute servers dataset which includes
a mixture of smaller commercial organizations and academic institutions
are very similar to those from our PlanetLab dataset.
Figure 15 shows the CDF of the distance between
the position estimate and the physical location of a node.
Octant again outperforms the other three techniques across the entire
set of targets, with a median localization error of 25 miles, compared
to 56 miles for GeoLim, 155 miles for GeoPing and 50 miles for GeoTrack.
The significant decrease in accuracy for GeoPing is likely due to
the reduction of landmarks from 51 in the PlanetLab dataset to
32 in the traceroute servers dataset, as GeoPing is the most sensitive
technique to the number of available landmarks.
These results show that Octant achieves high accuracy in its point
estimate for a target, high probability that its location estimate
will contain the target, and high precision as indicated by the size
of its location estimate area. Overall, Octant can locate the median
node to a point within 22 miles of its physical position, or to a
tight area (factor of two smaller than previous work) that contains
the physical location with 90% probability. Octant requires very few
landmarks to be effective; as few as 20 landmarks can achieve
approximately the same accuracy as from using all 50 landmarks.
6 CONCLUSIONS
Determining the geographic location of Internet hosts is an
intrinsically useful basic building block. Since there are no
existing standardized protocols for discovering the physical location
of endpoints, we must rely on techniques that can extract location
information from network measurements.
In this paper, we have outlined Octant,
a general, comprehensive framework for representing
network locations for nodes, extracting constraints on where nodes
may or may not be located, and combining these
constraints to compute small location estimates that bound
the possible location of target nodes with high
probability. Octant represents node position and regions precisely using
Bézier-bounded regions that can admit any kind of constraints,
makes use of both positive and negative information to aggressively
reduce the estimated region size, and can effectively reason in the
presence of uncertainty and erroneous constraints. It utilizes a
number of techniques to extract fine-grain information from end-to-end
latency measurements on the Internet.
We have evaluated our system using measurements from PlanetLab
hosts as well as public traceroute servers and found that
Octant is surprisingly accurate and effective. The framework can
localize the median node to within 22 miles of its actual position.
The evaluation also
indicates that Octant can localize a target to a region that is less
than half the size of previous approaches and contains the target
with much higher probability than the larger region. Octant enables
network operators to determine, with high confidence, the position of
nodes given simply latency measurements, which in turn enables
new location-aware services.
ACKNOWLEDGMENTS
We would like to thank our shepherd, T.S. Eugene Ng, and the anonymous
reviewers for many helpful comments and suggestions
4.
- 1
-
In this context, accuracy refers to the distance
between the computed point estimate and the actual location of the target.
In contrast, precision refers to the size of the region in
which a target is estimated to lie.
- 2
- An octant is a navigational
instrument used to obtain fixes.
- 3
- Note that this difference might embody some additional
transmission delays stemming from the use of indirect
paths. We expand on this in the next section.
- 4
- This work was supported in part by AF-TRUST (Air Force Team for Research
in Ubiquitous Secure Technology for GIG/NCES), which receives support
from the DAF Air Force Office of Scientific Research (#FA9550-06-1-0244)
and the following organizations: the National Science Foundation
(CCF-0424422) Cisco, British Telecom, ESCHER, HP, IBM, iCAST, Intel,
Microsoft, ORNL, Pirelli, Qualcomm, Sun, Symantec, Telecom Italia, and
United Technologies.
This document was translated from LATEX by
HEVEA.
|
