NSDI '06 Paper
[NSDI '06 Technical Program]
Subtleties in Tolerating
Correlated Failures
in Wide-area Storage Systems
Suman Nath1
Microsoft Research
sumann@microsoft.com |
Haifeng Yu
Phillip B. Gibbons
Intel Research Pittsburgh
{haifeng.yu,phillip.b.gibbons}@intel.com |
Srinivasan Seshan
Carnegie Mellon University
srini@cmu.edu |
Abstract:
High availability is widely accepted as an explicit requirement for
distributed storage systems. Tolerating correlated failures is a key
issue in achieving high availability in today's wide-area
environments. This paper systematically revisits previously proposed
techniques for addressing correlated failures. Using several
real-world failure traces, we qualitatively answer four important
questions regarding how to design systems to tolerate such failures.
Based on our results, we identify a set of design principles that
system builders can use to tolerate correlated failures. We show how
these lessons can be effectively used by incorporating them into
IrisStore, a distributed read-write storage layer that provides high
availability. Our results using IrisStore on the PlanetLab over an 8-month
period demonstrate its ability to withstand large correlated
failures and meet preconfigured availability targets.
1 Introduction
High availability is widely accepted as an
explicit requirement for distributed storage systems (e.g.,
[8, 9, 10, 14, 15, 19, 22, 41]). This is partly because
these systems are often used to store important data, and partly
because performance is no longer the primary limiting factor
in the utility of distributed storage systems. Under the assumption
of failure independence, replicating or erasure coding the data
provides an effective way to mask individual node failures. In
fact, most distributed storage systems today use some form of
replication or erasure coding.
In reality, the assumption of failure independence is rarely true.
Node failures are often correlated, with multiple nodes in the
system failing (nearly) simultaneously. The size of these
correlated failures can be quite large. For example, Akamai
experienced large distributed denial-of-service (DDoS) attacks on
its servers in May and June 2004 that resulted in the unavailability
of many of its client sites [1]. The PlanetLab
experienced four failure events during the first half of 2004 in
which more than 35 nodes (≈ 20%) failed within a few
minutes. Such large correlated failure events may have numerous
causes, including system software bugs, DDoS attacks, virus/worm
infections, node overload, and human errors. The impact of failure
correlation on system unavailability is dramatic (i.e., by orders of
magnitude) [6, 38].
As a result, tolerating correlated
failures is a key issue in designing highly-available distributed
storage systems.
Even though researchers have long been aware of correlated failures,
most systems [8, 9, 10, 14, 15, 40, 41] are still evaluated and compared under
the assumption of independent failures.
In the context of the IrisNet project [17], we aim
to design and implement a distributed read/write storage layer that
provides high availability despite correlated node failures in
non-P2P wide-area environments (such as the PlanetLab and Akamai).
We study three
real-world failure traces for such environments to evaluate the impact of realistic failure
patterns on system designs.
We frame our study around providing quantitative answers to
several important questions, some of which
involve the effectiveness of existing
approaches [19, 37].
We show that some existing approaches, although plausible, are less
effective than one might hope under real-world failure correlation,
often resulting in system designs that are far from optimal. Our
study also reveals the subtleties that cause this discrepancy
between the expected behavior and the reality. These new findings
lead to four design principles for tolerating correlated failures.
While some of the findings are perhaps less surprising than others,
none of the findings and design principles were
explicitly identified or carefully quantified prior to our work.
These design principles are applied and implemented in our
highly-available read/write storage layer called IrisStore.
Our study answers the following four questions about
tolerating correlated failures:
- Can correlated failures be avoided by history-based failure
pattern prediction? We find that
avoiding correlated failures by predicting the failure pattern based
on externally-observed failure history (as
proposed in OceanStore [37]) provides
negligible benefits in alleviating the negative effects of
correlated failures in our real-world failure traces. The subtle
reason is that the top 1% of correlated failures (in terms of size)
have a dominant effect on system availability, and their failure
patterns seem to be the most difficult to predict.
- Is simple modeling of failure sizes adequate? We find
that considering only a single (maximum) failure size (as in
Glacier [19]) leads to suboptimal system designs.
Under the same level of failure correlation, the system
configuration as obtained in [19] can be both
overly-pessimistic for lower availability targets (thereby wasting
resources) and overly-optimistic for higher availability targets
(thereby missing the targets). While it is obvious that simplifying
assumptions (such as assuming a single failure size) will always
introduce inaccuracy, our contribution is to show that the
inaccuracy can be dramatic in practical
settings. For example, in our traces, assuming a single failure
size leads to designs that either waste 2.4 times the needed
resources or miss the availability target by 2 nines. Hence, more
careful modeling is crucial.
We propose using a bi-exponential model to capture the distribution
of failure sizes, and show how this helps avoid overly-optimistic or
overly-pessimistic designs.
- Are additional fragments/replicas always effective in
improving availability? For popular (n/2)-out-of-n encoding
schemes (used in OceanStore [22] and
CFS [10]), as well as majority voting
schemes [35] over
n replicas, it is well known that
increasing n yields an exponential decrease in unavailability
under independent failures. In contrast, we find that under
real-world failure traces with correlated failures, additional
fragments/replicas result in a strongly diminishing return in
availability improvement for many schemes including the previous
two. It is important to note that this diminishing return does not directly result from the simple presence of correlated
failures. For example, we observe no diminishing return under
Glacier's single-failure-size correlation model. Rather, in our
real-world failure traces, the diminishing return arises due to the
combined impact of correlated failures of different sizes. We
further observe that the diminishing return effects are so strong
that even doubling or tripling n provides only limited benefits
after a certain point.
- Do superior designs under independent failures remain
superior under correlated failures? We find that the effects of
failure correlation on different designs are dramatically different.
Thus selecting between two designs D and
D'
based on their availability under independent failures may lead to
the wrong choice: D can be far superior under
independent failures but far inferior under real-world correlated
failures. For example, our results show that while 8-out-of-16
encoding achieves 1.5 more nines of availability than 1-out-of-4
encoding under independent failures, it achieves 2 fewer nines than
1-out-of-4 encoding under correlated failures. Thus, system designs
must be explicitly evaluated under correlated failures.
Our findings, unavoidably, depend on the failure traces we used.
Among the four findings, the first one may be the most dependent on
the specific traces. The other three findings, on the other hand,
are likely to hold as long as failure correlation is non-trivial and
has a wide range of failure sizes.
We have incorporated these lessons and design principles into our
IrisStore prototype:
IrisStore does not try to avoid correlated failures
by predicting the correlation pattern; it uses a failure size
distribution model rather than a single failure size; and it
explicitly quantifies and compares configurations via online
simulation with our correlation model. As an example application,
we built a publicly-available distributed wide-area network
monitoring system on top of IrisStore, and deployed it on over 450
PlanetLab nodes for 8
months. We summarize our performance and availability experience
with IrisStore, reporting its behavior during a highly unstable period
of the PlanetLab (right before the SOSP 2005 conference deadline), and
demonstrating its ability to reach a pre-configured availability
target.
2 Background and Related Work
Distributed storage systems and erasure coding.
Distributed storage systems [8, 9, 10, 14, 15, 19, 22, 41]
have long been an active area in systems research. Of these systems, only
OceanStore [22] and Glacier [19]
explicitly consider correlated failures. OceanStore
uses a distributed hash table (DHT) based design to
support a significantly larger user population (e.g., 1010 users)
than previous systems.
Glacier is a more robust version
of the PAST [32] DHT-based storage system that is explicitly
designed to tolerate correlated failures.
Distributed storage systems commonly use data redundancy
(replication, erasure coding [31]) to provide high
availability. In erasure coding, a data object is encoded into n
fragments, out of which any m fragments can reconstruct
the object. OceanStore uses (n/2)-out-of-n erasure coding.
This configuration of erasure coding is also used by the most
recent version of CFS [10, 13], one of the first
DHT-based, read-only storage systems. Glacier, on the other hand,
adapts the settings of m and n to achieve availability
and resource targets.
Replication can be viewed as a special case of erasure coding where m
= 1.
In large-scale systems, it is often desirable to automatically
create new fragments upon the loss of existing ones (due to
node failures). We call such systems regeneration
systems. Almost all recent distributed storage systems (including
OceanStore, CFS, and our IrisStore system) are regeneration
systems. Under the assumption of failure independence, the
availability of regeneration systems is typically analyzed [41] using a
Markov chain to model the birth-death process.
Previous availability studies of correlated failures. Traditionally,
researchers assume failure independence when studying
availability [8, 9, 10, 14, 15, 40, 41]. For storage systems,
correlated failures have recently
drawn more attention in the context of wide-area
environments [11, 19, 21, 37, 38], local-area and
campus network environments [9, 34], and disk
failures [6, 12].
None of these previous studies point out the findings and design
principles in this paper or quantify their effects.
Below, we focus on those works most relevant to our study that were not
discussed in the previous section.
The Phoenix Recovery Service [21] proposes
placing replicas on nodes running heterogeneous versions of software, to
better guard against correlated failures. Because their target
environment is a heterogeneous environment such as a peer-to-peer
system, their approach does not conflict with our findings.
The effects of correlated failures on erasure coding systems have
also been studied [6] in the context of survivable
storage disks. The study is based on availability traces of
desktops [9] and different Web servers. (We use the
same Web server trace in our study.) However, because the target
context in [6] is disk drives, the study considers
much smaller-scale systems (at most 10 disks) than we do.
Finally, this paper establishes a bi-exponential model to fit
correlated failure size distribution. Related to our work, Nurmi et
al. [30] show
that machine availability (instead of failure sizes)
in enterprise and wide-area distributed
systems also follows hyper-exponential (a more general version of our
bi-exponential model) models.
Data maintenance costs. In addition to availability,
failure correlation also impacts data maintenance costs (i.e.,
different amounts of data transferred over the network in
regenerating the objects). Weatherspoon et al. [36]
show that the maintenance costs of random replica placement
(with small optimizations) are similar to those of an idealized
optimal placement where failure correlation is completely avoided.
These results do not
conflict with our conclusion that random replica
placement (or even more sophisticated placement) cannot
effectively alleviate the negative effects of failure correlation on
availability.
3 Methodology
This study is based on system
implementation and experimental evaluation. The experiments use a
combination of three testbeds: live PlanetLab deployment,
real-time emulation on Emulab [2], and event-driven
simulation. Each testbed allows progressively more extensive
evaluation than the previous one. Moreover,
the results from one testbed help validate the results from the next testbed.
We report availability and
performance results from the 8-month live deployment of our system
over the PlanetLab. We also present detailed simulation results for
deeper understanding into system availability, especially when
exploring design choices. Simulation allows us to directly compare
different system configurations by subjecting them to identical
streams of failure/recovery events, which is not possible using
our live deployment. We have carefully validated the accuracy of
our simulation results by comparing them against the results from
the PlanetLab deployment and also Emulab emulation. Our detailed
comparison in [29] shows that there is
negligible differences between the three sets of results.
In this paper, we use Erasure(m,n) to denote an m-out-of-n
read-only erasure coding system. Also, to unify terminology, we
often refer to replicas as fragments of an Erasure(1,n) system.
Unless otherwise mentioned, all designs we discuss in this paper
use regeneration to compensate for lost fragments due to
node failures.
For the purpose of studying correlated failures, a failure event
(or simply failure) crashes one or more nodes in the system. The
number of nodes that crash is called the size of the failure. To
distinguish a failure event from the failures of individual nodes, we
explicitly call the latter node failures. A data object is unavailable if it can not be reconstructed due to failures.
We present availability results using standard “number of nines”
terminology (i.e., log0.1(ϕ), where ϕ is the
probability that the data object is unavailable).
| Trace |
Duration |
Nature of nodes |
# of nodes |
Probe
interval |
Probe method |
| PL_trace [3] |
03/2003 to 06/2004 |
PlanetLab nodes |
277 on avg |
15 to 20 mins |
all-pair pings; 10 ping packets per
probe |
| WS_trace [6] |
09/2001 to 12/2001 |
Public web
servers |
130 |
10 mins |
HTTP GET from a CMU machine |
| RON_trace [4] |
03/2003 to 10/2004 |
RON testbed |
30
on avg |
1 to 2 mins |
all-pair pings; 1 ping packet per probe |
Table 1: Three traces used in our study.
Failure traces. We use three real-world wide-area
failure traces (Table 1) in our study.
WS_trace is intended to be representative of public-access
machines that are maintained by different administrative domains,
while PL_trace and RON_trace potentially describe the behavior
of a centrally administered distributed system that is used mainly
for research purposes, as well as for a few long running services.
A probe interval is a complete round of all pair-pings or Web
server probes.
PL_trace2
and RON_trace consist of periodic probes between every pair of
nodes. Each probe may consist of multiple pings; we declare that a
node has failed if none of the other nodes can ping it
during that interval. We do not distinguish between whether the node
has failed or has simply been partitioned from all other nodes—in
either case it is unavailable to the overall system. WS_trace
contains logs of HTTP GET requests from a single node at CMU to
multiple Web servers. Our evaluation of this trace is not as precise
because near-source network partitions make it appear as if all the
other nodes have failed. To mitigate this effect, we assume that the
probing node is disconnected from the network if 4 or more
consecutive HTTP requests to different servers fail.3 We then
ignore all failures during that probe period. This heuristic may
still not perfectly classify source and server failures, but we
believe that the error is likely to be minimal.
In studying correlated failures, each probe interval is considered
as a separate failure event whose size is the number of failed
nodes that were available during the previous interval.
More details on our trace processing methodology can be found in
[29].
Limitations.
Although the findings from this paper depend on the traces we use,
the effects observed in this study are likely to hold as long as
failure correlation is non-trivial and has a wide range of failure sizes. One possible exception is our
observation about the difficulty in predicting failure patterns of
larger failures. However, we believe that the sources of some
large failures (e.g., DDoS attacks) make accurate prediction
difficult in any deployment.
Because we target IrisStore's design for non-P2P environments, we
intentionally study failure traces from systems with largely
homogeneous software (operating systems, etc.). Even in WS_trace,
over 78% of the web servers were using the
same Apache server running over Unix, according to the historical
data at http://www.netcraft.com. We believe that wide-area
non-P2P systems (such as Akamai) will largely be homogeneous because
of the prohibitive overhead of maintaining multiple versions of
software.
Failure correlation in P2P systems can be dramatically different from
other wide-area systems, because many failures in P2P systems are caused
by user departures. In the future, we plan to extend our study
to P2P environments. Another limitation of our traces is that the
long probe intervals prevent the detection of short-lived
failures. This makes our availability results slightly optimistic.
Steps in our study. Section 4
constructs a tunable failure correlation model from our three
failure traces; this model allows us to study the sensitivity of our
findings beyond the three traces.
Sections 5–8 present the questions
we study, and their corresponding answers, overlooked subtleties,
and design principles. These sections focus on read-only
Erasure(m,n) systems, and mainly use trace-driven simulation,
supplemented by model-driven simulation for sensitivity study.
Section 9 shows that our conclusions
readily extend to read/write systems.
Section 10 describes and evaluates
IrisStore, including its
availability running on PlanetLab for an 8-month period.
4 A Tunable Model for Correlated Failures
This section constructs a tunable failure correlation model from the
three failure traces. The primary purpose of this model is to allow
sensitivity studies and experiments with correlation levels that are
stronger or weaker than in the traces. In addition, the model later
enables us to avoid overly-pessimistic and overly-optimistic
designs. The model balances idealized assumptions (e.g., Poisson
arrival of correlated failures) with realistic characteristics
(e.g., mean-time-to-failure and failure size distribution) extracted
from the real-world traces. In particular, it aims to accurately
capture large (but rare) correlated failures, which have a dominant
effect on system unavailability.
4.1 Correlated Failures in Real Traces
We start by investigating the failure correlation in our three
traces. Figure 1 plots the PDF of failure event sizes for
the three traces.
Because of the finite length of the
traces, we cannot observe events with probability less than
10−5 or 10−6.
While RON_trace and WS_trace have a roughly constant node
count over their entire duration, there is a large variation in
the total number of nodes in PL_trace. To compensate, we use
both raw and normalized failure event sizes for PL_trace.
The normalized size is the (raw) size multiplied by a
normalization factor γ, where γ is the average number of nodes
(i.e., 277) in PL_trace divided by the number of
nodes in the interval.
In all traces, Figure 1 shows that
failure correlation has different strengths in two regions. In
PL_trace, for example, the transition between the two regions
occurs around event size 10.
In both regions, the probability decreases roughly exponentially
with the event size (note the log-scale of the y-axis). However, the
probability decreases significantly faster for small-scale
correlated failures than for large-scale ones. We call such a
distribution bi-exponential. Although we have only anecdotal
evidence, we conjecture that different failure causes are
responsible for the different parts of the distribution. For
example, we believe that system instability, some application
bugs, and localized network partitions are responsible for the
small failure events. It is imaginable that the probability
decreases quickly as the scale of the failure increases.
On the other hand, human interference, attacks, viruses/worms and
large ISP failures are likely to be responsible for the large
failures. This is supported by the fact that many of the larger
PlanetLab failures can be attributed to DDoS attacks (e.g., on
12/17/03), system software bugs (e.g., on 3/17/04), and node overloads
(e.g., on 5/14/04). Once such a problem reaches a certain scale,
extending its scope is not much harder. Thus, the probability
decreases relatively slowly as the scale of the failure increases.
4.2 A Tunable Bi-Exponential Model
In our basic failure model, failure events arrive at the system
according to a Poisson distribution. The entire system has a universe of u nodes. The model does not explicitly specify
which of the u nodes each failure event crashes, for the
following reasons:
Predicting failure patterns is not an effective means for improving
availability, and pattern-aware fragment placement achieves almost
identical availability as a pattern-oblivious random placement
(see Section 5). Thus, our availability
study needs to consider only the case where the m fragments of a
data object are placed on a random set of m nodes. Such a random
placement, in turn, is equivalent to using a fixed set of m nodes
and having each failure event (with size s) crash a random set of
s nodes in the universe. Realizing the above point helps us to avoid
the unnecessary complexity of modeling which nodes each failure event
crashes – each failure event simply crashes a random set of s
nodes.
We find that many existing distributions (such as
heavy-tail distributions [24]) cannot capture the
bi-exponential property in the trace. Instead, we use a model that has
two exponential components, one for each region. Each component
has a tunable parameter ρ between 0 and ∞ that
intuitively captures the slope of the curve and controls how
strong the correlations are. When ρ=0, failures are
independent, while ρ=∞ means that every failure event
causes the failure of all u nodes. Specifically, for 0 < ρ <
∞, we define the following geometric sequence: f(ρ,i) =
c(ρ) ⋅ ρi. The normalizing factor c(ρ) serves
to make Σi=0u f(ρ, i) = 1.
We can now easily capture the bi-exponential property by composing
two f(ρ,i). Let pi be the probability of failure events of
size i, for 0 ≤ i ≤ u. Our
correlation model, denoted as G(α, ρ1, ρ2), defines
pi = (1−α) f(ρ1, i) + α f(ρ2, i),
where α is a tunable parameter that describes the
probability of large-scale correlated failures. Compared to a
piece-wise function with different ρ's for the two regions,
G(α, ρ1, ρ2) avoids a sharp turning point at the
boundary between the two regions.
Figure 1 shows how well this model fits the three
traces. The parameters of the models are chosen such that the Root
Mean Square errors between the models and the trace points are
minimized. Because of space limitations, we are only able to
provide a brief comparison among the traces here. The parameters
of the model are different across the traces, in large part
because the traces have different universe sizes (10 node failures out
of 277 nodes is quite different from 10 node failures out of 30 nodes).
As an example of a more fair comparison, we selected 130 random
nodes from PL_trace to enable a comparison with WS_trace,
which has 130 nodes. The resulting trace is well-modeled by
G(0.009, 0.3, 0.96). This means that the probability of
large-scale correlated failures in PL_trace is about 8 times
larger than WS_trace.
Failure arrival rate and recovery. So far
the correlation model G(α, ρ1, ρ2) only describes
the failure event size distribution, but does
not specify the event arrival rate. To study the effects of
different levels of correlation, the event arrival rate should be
such that the average mean-time-to-failure (MTTF) of nodes in the
traces is always preserved. Otherwise with a constant failure
event arrival rate, increasing the correlation level would have the
strong side effect of decreasing node MTTFs. To preserve the
MTTF, we determine the system-wide failure event arrival rate
λ to be such that 1/(λ Σi=1u(ipi)) = MTTF/u.
We observe from the traces that, in fact, there exists non-trivial
correlation among node recoveries as well. Moreover, nodes in the
traces have non-uniform MTTR and MTTF. However, our experiments
show that the above two factors have little impact on system
availability for our study. Specifically, for all parameters we
tested (e.g., later in Figure 4), the availability
obtained under model-driven simulation
(which assumes independent recoveries and uniform MTTF/MTTR) is
almost identical to that obtained under trace-driven simulation (which
has recovery correlation and non-uniform MTTF/MTTR).
Therefore, our model
avoids the unnecessary complexity of modeling recovery correlation
and non-uniform MTTF/MTTR.
Stability of the model. We have performed
an extensive stability study for our model
using PL_trace and
RON_trace. We do not use WS_trace due to its short length. We
summarize our results below – see [29] for
the full results. Our results show that each model converges within
a 4 month period in its respective failure traces. We believe this
convergence time is quite good given the rarity of large
correlation events. Second, the model built (“trained”) using a
prefix of a trace (e.g., the year 2003 portion) reflects well the
failures occurring in the rest of the trace (e.g., the year 2004
portion).
This is
important because we later use the model to configure
IrisStore to
provide a given availability target.
In the next four sections, we will address each of the four questions
from Section 1. Unless otherwise
stated, all our results are obtained via event-driven simulation
(including data regeneration) based on the three real failure
traces. The bi-exponential model is used only when we need to tune
the correlation level—in such cases we will explicitly mention its
use. As mentioned earlier, the accuracy of our simulator has been
carefully validated against live deployment
results on the PlanetLab and also emulation results on Emulab. Because
many existing systems (e.g., OceanStore, Glacier, and CFS) use a
large number of fragments, we show results for up to n=60
fragments (as well as for large values of m).
5 Can Correlated Failures be Avoided by History-based Failure
Pattern Prediction?
Chun et al. [11] point out that
externally observed node failure histories (based on probing)
can be used to discover a relatively stable
pattern of correlated failures (i.e., which set of nodes tend to
fail together), based on a portion of PL_trace.
Weatherspoon et al. [37] (as
part of the OceanStore project [22]) reach a similar
conclusion by analyzing a four-week failure trace of 306 web
servers4. Based on such
predictability, they further propose a framework for online
monitoring and clustering of nodes. Nodes within the same cluster
are highly correlated, while nodes in different clusters are more
independent. They show that the clusters constructed from the first
two weeks of their trace are similar to those constructed from the
last two weeks. Given the stability of the clusters, they conjecture
that by placing the n fragments (or replicas) in n different
clusters, the n fragments will not observe excessive failure
correlation among themselves. In some sense, the problem of
correlated failures goes away.
Our Finding. We carefully quantify the effectiveness of
this technique using the same method as
in [37] to process our failure
traces.
For each trace, we use the first half of the trace (i.e., “training
data”) to cluster the nodes using the same clustering
algorithm [33] as used
in [37].
Then, as a case study, we consider two placement schemes of an
Erasure(n/2, n) (as in OceanStore) system. The first scheme (pattern-aware) explicitly places the n fragments of the same
object in n different clusters, while the second scheme (pattern-oblivious) simply places the fragments on n random
nodes. Finally, we measure the availability under the second half of
the trace.
We first observe that most (≈ 99%) of the failure events
in the second half of the traces affect only a very small number
(≤ 3) of the clusters computed from the first half of the
trace. This implies that the clustering of correlated nodes is
relatively stable over the two halves of the traces, which is
consistent with [37].

Figure 2:
Negligible
availability improvements from failure pattern prediction of
WS_trace for Erasure(n/2, n) systems.
On the other hand, Figure 2 plots the
achieved availability of the two placement schemes under
WS_trace. PL_trace produces similar
results [29].
We do not use RON_trace because it contains too few nodes.
The graph shows that explicitly
choosing different clusters to place the fragments gives us negligible improvement on availability. We also plot the
availability achieved if the failures in WS_trace were
independent. This is done via model-driven simulation and by setting
the parameters in our bi-exponential model accordingly.
Note that under independent failures, the two
placement schemes are identical. The large
differences between the curve for independent failures and the other
curves show that there are strong negative effects from failure
correlation in the trace. Identifying and exploiting failure
patterns, however, has almost no effect in alleviating such impacts.
We have also obtained similar findings under a wide-range of other
m and n values for Erasure(m,n).
A natural question is whether the above findings are
because our traces are different from the traces studied in
[11, 37]. Our PL_trace
is, in fact, a superset of the failure trace used in
[11]. On the other hand, the failure trace
studied in [37], which we call
Private_trace, is not publicly available. Is it possible that
Private_trace gives even better failure pattern predictability than
our traces, so that pattern-aware placement would indeed be
effective? To answer this question, we directly compare the
“pattern predictability” of the traces using the metric from
[37]: the average mutual
information among the clusters (MI) (see
[37] for a rigorous definition).
A smaller MI means that the clusters constructed from the training
data predict the failure patterns in the rest of the trace better.
Weatherspoon et al. report an MI of 0.7928 for their Private_trace.
On the other hand, the MI for our WS_trace is
0.7612. This means that the failure patterns in WS_trace are
actually more “predictable” than in Private_trace.
The Subtlety. To understand the above seemingly contradictory
observations, we take a deeper look at the
failure patterns. To illustrate, we classify the failures into
small failures and large failures based on whether the failure
size exceeds 15.
With this classification, in all traces, most (≈ 99%) of the
failures are small.
 |
|
 |
|
 |
| (a) Small failures in WS_trace |
|
(b) Large failures in
WS_trace |
|
(c) Large failures in RON_trace |
Figure 3:
Predictability of pairwise
failures. For two nodes selected at random, the plots show the
probability that the pair fail together (in correlation) more
than x times during the entire trace. Distributions fitting the
curves are also shown.
Next, we investigate how accurately we can predict the failure
patterns for the two classes of failures. We use the same
approach [20] used for showing that UNIX processes running for
a long time are more likely to continue to run for a long time.
For a random pair of nodes in WS_trace,
Figure 3(a) plots the probability that the pair
crashes together (in correlation) more than x times because of
the small failures. The straight line in log-log scale indicates
that the data fits the Pareto distribution of P(#failure ≥ x)=
cx−k, in this case for k=1.5. We observe similar fits for
PL_trace (P(#failure ≥ x)= 0.3x−1.45) and RON_trace
(P(#failure ≥ x) = 0.02x−1.4). Such a fit to the Pareto
distribution implies that
pairs of nodes that have failed together many times in the past
are more likely to fail together in the future [20].
Therefore, past pairwise failure patterns (and hence the
clustering) caused by the small failures are likely to hold in the
future.
Next, we move on to large failure events
(Figure 3(b)). Here, the data fit an
exponential distribution of P(#failure ≥ x)=a e−bx. The
memoryless property of the exponential distribution means that the
frequency of future correlated failures of two nodes is
independent of how often they failed together in the past. This in
turn means that we cannot easily (at least using existing history-based
approaches) predict the failure patterns caused by these large
failure events. Intuitively, large failures are generally caused
by external events (e.g., DDoS attacks), occurrences of which are
not predictable in trivial ways.
We observe similar results [29] in the
other two traces.
For example, Figure 3(c) shows
an exponential distribution fit for the large failure events in
RON_trace. For PL_trace, the fit is P(#failure ≥
x)=0.3e−0.9x.
Thus, the pattern for roughly 99% of the failure events (i.e.,
the small failure events) is predictable, while the pattern for the
remaining 1% (i.e., the large failure events) is not easily predictable.
On the other hand, our experiments show that large failure events,
even though they are only 1% of all failure events, contribute the
most to unavailability. For example, the unavailability of a
“pattern-aware” Erasure(16, 32) under WS_trace remains unchanged
(0.0003) even if we remove all the small failure events.
The reason is that because small
failure events affect only a small number of nodes, they
can be almost completely masked by data redundancy and
regeneration. This explains why on the one hand, failure patterns are
largely predictable, while on the other hand, pattern-aware
fragment placement is not effective in improving availability. It
is also worth pointing out that the sizes of these large failures
still span a wide range (e.g., from 15 to over 50 in PL_trace
and WS_trace). So capturing the distribution over
all failure sizes is still important in the bi-exponential model.
The Design Principle. Large correlated failures (which
comprise a small fraction of all failures) have a dominant effect
on system availability, and system designs must not overlook these
failures. For example, failure pattern prediction techniques that
work well for the bulk of correlated failures but fail for large
correlated failures are not effective in alleviating the
negative effects of correlated failures.
Can Correlated Failures be Avoided by Root Cause-based Failure
Pattern Prediction?
We have established above that failure pattern prediction based on
failure history may not be effective. By identifying the root causes
of correlated failures, however, it becomes possible to predict
their patterns in some cases [21]. For example,
in a heterogeneous environment, nodes running the same OS may fail
together due to viruses exploiting a common vulnerability.
On the other hand, first,
not all root causes result in correlated failures with
predictable patterns. For example, DDoS attacks result in correlated
failures patterns that are inherently unpredictable.
Second, it can be challenging to identify/predict root causes for
all major correlated failures based on intuition. Human intuition does not
reason well about close-to-zero probabilities [16]. As a
result, it can be difficult to enumerate all top root causes. For
example, should power failure be
considered when targeting 5 nines availability? How about a certain
vulnerability in a certain software? It is always possible to miss
certain root causes that lead to major failures.
Finally, it can also be challenging to identify/predict root causes
for all major
correlated failures, because the frequency of individual root causes can
be extremely low. In some cases, a root cause may only demonstrate itself
once (e.g., patches are usually installed after vulnerabilities are
exploited).
For the above reasons, we believe that while root cause analysis
will help to make correlated failures more predictable, systems may
never reach a point where we can predict all major correlated
failures.
6 Is Simple Modeling of Failure Sizes Adequate?
A key challenge in system design is to obtain
the “right” set of parameters that will be neither
overly-pessimistic nor overly-optimistic in achieving given design
goals.
Because of the complexity in availability estimation introduced by
failure correlation, system designers sometimes make simplifying
assumptions on correlated failure sizes in order to make the problem
more amenable. For example, Glacier [19]
considers only the (single) maximum failure size, aiming to achieve
a given availability target despite the correlated failure of up to
a fraction f of all the nodes. This simplifying assumption enables
the system to use a closed-form formula [19] to
estimate availability and then calculate the needed m and n
values in Erasure(m,n).

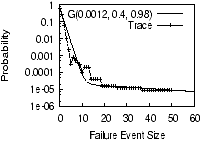
Figure 4: Number of fragments in
Erasure(6,n) needed to achieve certain availability targets, as
estimated by Glacier's single failure size model and our
distribution-based model of G(0.0012,0.4,0.98). We also plot the
actual achieved availability under the trace.
Our Finding. Figure 4 quantifies the effectiveness of
this approach. The figure plots the number
of fragments needed to achieve given availability targets under
Glacier's model (with f = 0.65 and f = 0.45) and under
WS_trace. Glacier does not explicitly explain how f can be
chosen in various systems. However, we can expect that f should be
a constant under the same deployment context (e.g., for WS_trace).
A critical point to observe in Figure 4 is that
for the real trace, the curve is not a straight line (we will explore
the shape of this curve later). Because the curves from Glacier's
estimation are roughly straight lines, they always significantly
depart from the curve under the real trace, regardless of how we
tune f. For example, when f = 0.45, Glacier over-estimates
system availability when n is large: Glacier would use
Erasure(6, 32) for an availability target of 7 nines, while in
fact, Erasure(6, 32) achieves only slightly above 5 nines
availability. Under the same f, Glacier also under-estimates the
availability of Erasure(6, 10) by roughly 2 nines. If f is
chosen so conservatively (e.g., f = 0.65) that Glacier never
over-estimates, then the under-estimation becomes even more
significant. As a result, Glacier would suggest Erasure(6, 31) to
achieve 3 nines availability while in reality, we only need to
use Erasure(6, 9). This would unnecessarily increase the bandwidth needed to create,
update, and repair the object, as well as the storage overhead, by over 240%.
While it is obvious that simplifying assumptions (such as
assuming a single failure size) will always introduce inaccuracy, our
above results show that the inaccuracy can be dramatic (instead
of negligible) in practical settings.
The Subtlety. The reason behind the above mismatch
between Glacier's estimation and the actual availability under
WS_trace is that in real systems, failure sizes may cover a
large range. In the limit, failure events of any size may occur;
the only difference is their likelihood. System availability is
determined by the combined effects of failures with different
sizes. Such effects cannot be summarized as the effects of a
series of failures of the same size (even with scaling factors).
To avoid the overly-pessimistic or overly-optimistic
configurations resulting from Glacier's method, a system must
consider a distribution of failure sizes.
IrisStore uses the bi-exponential model for this
purpose. Figure 4 also shows
the number of fragments needed for a given availability target as
estimated by our simulator driven by the bi-exponential model.
The estimation based on our model matches the curve from
WS_trace quite well. It is also important to note that the
difference between Glacier's estimation and our estimation is
purely from the difference between single failure size and a
distribution of failure sizes. It is not because Glacier uses a
formula while we use simulation. In fact, we have also performed
simulations using only a single failure size, and the results are similar
to those obtained using Glacier's formula.
The Design Principle.
Assuming a single failure size can result in dramatic rather than
negligible inaccuracies in practice. Thus correlated failures
should be modeled via a distribution.
7 Are Additional Fragments Always Effective in Improving
Availability?
Under independent failures, distributing the data always helps to
improve availability, and any target availability can be achieved by
using additional (smaller) fragments, without
increasing the storage overhead. For this reason, system designers
sometimes fix the ratio between n and m (so that the storage
overhead, n/m, is fixed), and then simply increase n and m
simultaneously to achieve a target availability.
For instance, under independent failures,
Erasure(16, 32) gives better availability than Erasure(12,
24), which, in turn, gives better availability than Erasure(8,
16). Several existing systems, including OceanStore and CFS, use
such Erasure(n/2, n) schemes.
Given independent failures, it can even be
proved [29] that increasing the number of
fragments (while keeping storage constant) exponentially
decreases unavailability. In Section 9, we will
show that a read/write replication system using majority
voting [35] for consistency has the same availability as
Erasure(n/2, n). Thus, our discussion in this section also applies to
these read/write replication systems (where, in this case, the storage
overhead does increase with n).
| |
 |
 |
| (a) Erasure(m, n) |
(b) Erasure(n/2,n) under |
(c) Erasure(n/2,n) under |
| under PL_trace |
one failure size |
two failure sizes |
Figure 5: Availability of Erasure(m,n) under different correlated
failures. In (b) and (c), the legend fx denotes correlated
failures of x fraction of all nodes in the system, and qfx
denotes fx happening with probability q.
Our Finding. We observe that distributing fragments across
more and more machines (i.e., increasing n) may not be effective under correlated
failures, even if we double or triple n.
Figure 5(a) plots the availability of
Erasure(4,n), Erasure(n/3,n) and Erasure(n/2, n) under
PL_trace. The graphs for WS_trace are similar
(see [29]). We do not use RON_trace because it
contains only 30 nodes. The three schemes clearly incur different
storage overhead and achieve different availability. We do not
intend to compare their availability under a given n value.
Instead, we focus on the scaling trend (i.e., the availability
improvement) under the three schemes when we increase n.
Both Erasure(n/3,n) and Erasure(n/2,n) suffer from a strong
diminishing return effect. For example, increasing n from 20 to
60 in Erasure(n/2,n) provides less than a half nine's improvement.
On the other hand, Erasure(4, n) does not suffer from such an
effect. By tuning the parameters in the correlation model and using
model-driven simulation, we further observe that the diminishing
returns become more prominent under stronger correlation levels as
well as under larger m values
[29]
.
The above diminishing return shows that correlated failures prevent a
system from effectively improving availability by distributed data
across more and more machines. In read/write systems using
majority voting, the problem is even worse: the same
diminishing return effect occurs despite the significant
increases in storage overhead.
The Subtlety.
It may appear that diminishing return is an obvious consequence of
failure correlation. However, somewhat surprisingly, we find that
diminishing return does not directly result from the
presence of failure correlation.
Figure 5(b) plots the availability of
Erasure(n/2, n) under synthetic correlated failures. In these
experiments, the system has 277 nodes total (to match the system
size in PL_trace), and each synthetic correlated failure crashes a
random set of nodes in the system.5 The synthetic
correlated failures all have the same size. For example, to obtain
the curve labeled “f0.2”, we inject correlated failure events
according to Poisson arrival, and each event
crashes 20% of the 277 nodes in the system. Using
single-size correlated failures matches the correlation model
used in Glacier's configuration analysis.
Interestingly, the curves in Figure 5(b)
are roughly straight lines and exhibit no diminishing returns. If we
increase the severeness (i.e., size) of the correlated failures, the
only consequence is smaller slopes of the lines, instead of
diminishing returns. This means that diminishing return does not
directly result from correlation. Next we explain that diminishing
return actually results from the combined effects of failures with
different sizes (Figure 5(c)).
Here we will discuss unavailability instead of availability, so that
we can “sum up” unavailability values. In the real world, correlated
failures are likely to have a wide range of sizes, as observed from
our failure traces. Furthermore, larger failures tend to be rarer than
smaller failures. As a rough approximation, system unavailability can
be viewed as the summation of the unavailability caused by failures
with different sizes. In Figure 5(c), we
consider two different failure sizes (0.2× 277 and 0.4 ×
277), where the failures with the larger size occur with smaller
probability. It is interesting to see that when we add up the
unavailability caused by the two kinds of failures, the resulting
curve is not a straight line.6 In fact, if we consider nines of
availability (which flips the curve over), the combined curve shows exactly
the diminishing return effect.
Given the above insight, we believe that diminishing returns are
likely to generalize beyond our three traces. As long as
failures have different sizes and as long as larger failures are rarer
than smaller failures, there will likely be diminishing returns.
The only way to lessen diminishing returns is to
use a smaller m in Erasure(m,n) systems. This will make the
slope of the line for 0.01f0.4 in
Figure 5(c) more negative, effectively
making the combined curve straighter.
The Design Principle. System designers should be aware that
correlated failures result in strong diminishing return effects in
Erasure(m,n) systems unless m is kept small. For popular systems
such as Erasure(n/2,n), even doubling or tripling n provides very
limited benefits after a certain point.
8 Do Superior Designs under Independent Failures Remain
Superior under Correlated Failures?
Traditionally, system designs are evaluated and compared under the
assumption of independent failures. A positive answer to this question
would provide support for this approach.

Figure 6: Effects of the
correlation model G(0.0012, 2/5ρ2, ρ2) on two
systems. ρ2=0 indicates independent failures, while
ρ2=0.98 indicates roughly the correlation level observed in
WS_trace.
Our Finding. We find that correlated failures hurt some
designs much more than
others. Such non-equal effects are demonstrated via the example in
Figure 6. Here, we plot the unavailability of
Erasure(1,4) and Erasure(8,16) under different failure
correlation levels, by tuning the parameters in our correlation
model in model-driven simulation. These experiments use the model G(0.0012,
2/5ρ2, ρ2) (a generalization of the model for WS_trace
to cover a range of ρ2), and a universe of 130 nodes, with MTTF
= 10 days and MTTR = 1 day. Erasure(1,4) achieves around 1.5
fewer nines than Erasure(8, 16) when failures are independent
(i.e., ρ2 = 0). On the other hand, under the correlation
level found in WS_trace (ρ2=0.98), Erasure(1,4) achieves
2 more nines of availability than Erasure(8, 16).7
The Subtlety. The cause of this (perhaps
counter-intuitive) result is the diminishing return effect
described earlier. As the correlation level increases, Erasure(8,
16), with its larger m, suffers from the
diminishing return effect to a much greater degree than Erasure(1, 4). In
general, because diminishing return effects are stronger for
systems with larger m, correlated failures hurt systems with
large m more than those with small m.
The Design Principle.
A superior design under independent failures may not be superior
under correlated failures. In particular, correlation hurts
systems with larger m more than those with smaller m.
Thus designs should be explicitly evaluated and
compared under correlated failures.
9 Read/Write Systems
Thus far, our discussion has focused on read-only Erasure(m,n)
systems. Interestingly, our results extend quite naturally to
read/write systems that use quorum techniques or voting techniques
to maintain data consistency.
Quorum systems (or voting systems) [7, 35] are
standard techniques for maintaining consistency for read/write
data. We first focus on the case of pure replication. Here, a user
reading or writing a data object needs to access a quorum
of replicas. For example, the majority quorum system (or majority
voting) [35] requires that the user accesses a
majority of the replicas. This ensures that any reader
intersects in at least one replica with the latest writer, so
that the reader sees the
latest update. If a majority of the replicas is not available,
then the data object is unavailable to the user. From an
availability perspective, this is exactly the same as a read-only
Erasure(n/2, n) system. Among all quorum systems that always
guarantee consistency, we will consider only majority voting
because its availability is provably optimal [7].
Recently, Yu [40] proposed signed quorum systems
(SQS), which uses quorum sizes smaller than n/2, at the cost of a
tunably small probability of reading stale data. Smaller quorum
sizes help to improve system availability because fewer replicas
need to be available for a data object to be available. If we do not
consider regeneration (i.e, creating new replicas to compensate for
lost replicas), then the availability of such SQS-based systems
would be exactly the same as that of a read-only Erasure(m, n)
system, where m is the quorum size.
Regeneration makes the problem slightly more complex, but our design
principles still apply [29].
Finally, quorum systems can also be used over erasure-coded
data [18]. Despite the complexity of these protocols, they
all have simple threshold-based requirements on the number of
available fragments. As a result, their availability can also be
readily captured by properly adjusting the m in our Erasure(m,n)
results.
10 IrisStore: A Highly-Available Read/Write Storage Layer
Applying the design principles in the previous sections, we have built
IrisStore, a decentralized read/write storage layer that is
highly-available despite correlated failures.
IrisStore does not try to
avoid correlated failures by predicting correlation patterns. Rather, it
tolerates them by choosing the right set of parameters.
IrisStore
determines system parameters using a model with a failure size
distribution rather than a single failure size. Finally,
IrisStore explicitly
quantifies and compares configurations via online simulation using our
correlation model. IrisStore allows both replication and erasure coding
for data redundancy, and also implements both majority quorum systems
and SQS for data consistency. The original design of
SQS [40] appropriately
bounds the probability of inconsistency (e.g., probability of stale
reads) when nodes MTTF and MTTR are
relatively large compared to the inter-arrival time between writes and
reads. If MTTF and MTTR are small compared to the write/read inter-arrival
time, the inconsistency may be
amplified [5]. To avoid such undesirable amplification,
IrisStore
also incorporates a simple data refresh technique [28].
We use IrisStore as the read-write storage layer of
IrisLog8, a
wide-area network monitoring system deployed on over 450+
PlanetLab nodes. IrisLog with
IrisStore has been available for
public use for over 8 months.
At a high level, IrisStore consists of two major components. The first
component replicates or encodes objects, and processes user
accesses. The second component is responsible for regeneration, and
automatically creates new fragments when existing ones fail. These
two subsystems have designs similar to Om [41]. For lack
of space, we omit the details (see [26]) and focus
on two aspects that are unique to
IrisStore.
10.1 Achieving Target Availability
Applications configure
IrisStore by specifying an availability
target, a bi-exponential failure correlation model, as well
as a cost function. The correlation model can be specified
by saying that the deployment context is “PlanetLab-like,”
“WebServer-like,” or “RON-like.” In these cases,
IrisStore will
use one of the three built-in failure correlation models from
Section 4. We also intend to add more
built-in failure correlation models in the future. To provide more
flexibility, IrisStore also allows the application to directly
specify the three tunable parameters in the bi-exponential
distribution. It is our long term goal to extend
IrisStore to monitor
failures in the deployment, and automatically adjust the
correlation model if the initial specification is not accurate.
The cost function is an application-defined function that
specifies the overall cost resulting from performance overhead and
inconsistency (for read/write data). The function takes three inputs, m,
n, and i (for inconsistency), and returns a cost value that
the system intends to minimize given that the availability target
is satisfied. For example, a cost function may bound the storage
overhead (i.e., n/m) by returning a high cost if n/m exceeds
certain threshold. Similarly, the application can use the cost
function to ensure that not too many nodes need to be contacted to
retrieve the data (i.e., bounding m). We choose to leave the
cost function to be completely application-specific because the
requirements from different applications can be dramatically
different.
With the cost function and the correlation model,
IrisStore uses
online simulation to determine the best values for m, n, and
quorum sizes. It does so by exhaustively searching the parameter
space (with some practical caps on n and m), and picking the
configuration that minimizes the cost function while still
achieving the availability target. The amount of inconsistency
(i) is predicted [39, 40] based on the quorum size.
Finally, this best configuration is used to instantiate the
system.
Our simulator takes around 7 seconds for each configuration
(i.e., each pair of m and n values) on a single 2.6GHz Pentium
4; thus IrisStore can perform a brute-force exhaustive search for
20,000 configurations (i.e., a cap of 200 for both n and m, and
m ≤ n) in about one and a half days. Many optimizations are
possible to further prune the search space.
For example, if Erasure(16,32) does not reach the availability target
then neither does Erasure(17,32). This exhaustive search is performed
offline; its overhead does not affect system performance.
10.2 Optimizations for Regeneration
When regenerating read/write data,
IrisStore (like
RAMBO [25] and Om [41]) uses the Paxos
distributed consensus protocol [23] to ensure
consistency. Using such consistent regeneration techniques in the
wide-area, however, poses two practical challenges that are not
addressed by RAMBO and Om:9
Flooding problem. After a large correlated failure,
one instance of the Paxos protocol needs to be executed for each
of the objects that have lost any fragments.
For example, our IrisLog deployment on the PlanetLab has 3530
objects storing PlanetLab sensor data, and each object has 7
replicas. A failure of 42 out of 206 PlanetLab nodes (on
3/28/2004) would flood the system with 2,478 instances of Paxos. Due
to the message complexity of Paxos,
this creates excessive overhead and stalls the entire system.
Positive feedback problem. Determining whether a
distant node has failed is often error-prone due to unpredictable
communication delays and losses. Regeneration activity after a
correlated failure increases the inaccuracy of failure detection
due to the increased load placed on the network and nodes.
Unfortunately, inaccurate failure detections trigger more
regeneration which, in turn, results in larger inaccuracy. Our
experience shows that this positive feedback loop can easily crash
the entire system.
To address the above two problems,
IrisStore implements two
optimizations:
Opportunistic Paxos-merging.
In IrisStore, if the system needs to invoke Paxos for multiple objects
whose fragments happen to reside on the same set of nodes, the
regeneration module merges all these Paxos invocations into a single
one. This approach is particularly effective with
IrisStore's load
balancing algorithm [27], which tends to place the
fragments for two objects either on the same set of nodes or on
completely disjoint sets of nodes. Compared to explicitly aggregating
objects into clusters, this approach avoids the need to maintain
consistent split and merge operations on clusters.
Paxos admission-control. To avoid the positive feedback
problem, we use a simple admission control mechanism on each node to
control its CPU and network overhead, and to avoid excessive false
failure detections. Specifically, each node, before initiating a
Paxos instance, samples (by piggybacking on the periodic ping
messages) the number of ongoing Paxos instances on the relevant
nodes. Paxos is initiated only if the average and the maximum number
of ongoing Paxos instances are below some thresholds (2 and 5,
respectively, in our current deployment). Otherwise, the node
queues the Paxos instance and backs off for some random time before
trying again.
Immediately before a queued Paxos is started,
IrisStore rechecks whether
the regeneration is still necessary (i.e., whether the object is still
missing a fragment). This further improves failure detection accuracy,
and also avoids regeneration when the failed nodes have already
recovered.
10.3 Availability of
IrisStore in the Wild
In this section and the next, we report our availability
and performance experience with IrisStore (as part of
IrisLog) on the PlanetLab over an 8-month period. IrisLog uses
IrisStore to maintain 3530 objects for different
sensor data collected from PlanetLab nodes. As a background testing
and logging mechanism, we continuously issued one query to
IrisLog every five minutes. Each query tries
to access all the objects stored in
IrisStore. We set a target
availability of 99.9% for our deployment, and
IrisStore chooses,
accordingly, a replica count of 7 and a quorum size of 2.
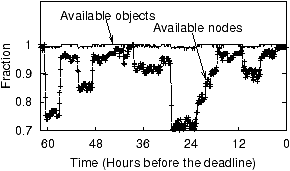
Figure 7: Availability of
IrisStore in the wild.
Figure 7 plots the behavior of our deployment
under stress over a 62-hour period, 2 days before the SOSP'05 deadline
(i.e., 03/23/2005).
The PlanetLab tends to suffer the most failures and instabilities right
before major conference deadlines. The figure shows both the
fraction of available nodes in the PlanetLab and the fraction of
available (i.e., with accessible quorums) objects in
IrisStore.
At the beginning of the period, IrisStore was running on around 200
PlanetLab nodes. Then, the PlanetLab experienced a number of large correlated
failures, which correspond to the sharp drops in the “available
nodes” curve (the lower curve). On the other hand, the fluctuation
of the “available objects” curve (the upper curve) is consistently
small, and is always above 98% even during such an unusual stress
period. This means that our real world
IrisStore deployment tolerated
these large correlated failures well. In fact, the overall
availability achieved by IrisStore during the 8-month deployment was
99.927%, demonstrating the ability of
IrisStore to achieve a
pre-configured target availability.
10.4 Basic Performance of
IrisStore
 |
 |
 |
| (a) End-to-end latency |
(b) Bandwidth consumption |
(c) Avg. # of replicas per object |
Figure 8:
IrisStore performance. (In (c), “AC”
means Paxos admission-control and “PM” means Paxos-merging.)
Access latency.
Figure 8(a) shows the measured latency from our lab
to access a single object in our IrisLog deployment. The object
is replicated on random PlanetLab nodes. We study two different
scenarios based on whether the replicas are within the US or all
over the world. Network latency contributes to most of the
end-to-end latency, and also to the large standard deviations.
Bandwidth usage. Our next experiment studies the amount
of bandwidth consumed by regeneration, including the Paxos
protocol. To do this, we consider the PlanetLab failure event on
3/28/2004 that caused 42 out of the 206 live nodes to crash in a
short period of time (an event found by analyzing PL_trace). We
replay this event by deploying IrisLog on 206 PlanetLab nodes
and then killing the IrisLog process on 42 nodes.
Figure 8(b) plots the bandwidth used during
regeneration. The failures are injected at time 100. We observe
that on average, each node only consumes about 3KB/sec bandwidth,
out of which 2.8KB/sec is used to perform necessary regeneration,
0.27KB/sec for unnecessary regeneration (caused by false failure
detection), and 0.0083KB/sec for failure detection (pinging). The
worst-case peak for an individual node is roughly 100KB/sec, which
is sustainable even with home DSL links.
Regeneration time. Finally, we study the amount of time
needed for regeneration, demonstrating the importance of our
Paxos-merging and Paxos admission-control optimizations.
We consider the same failure event (i.e.,
killing 42 out of 206 nodes) as above.
Figure 8(c) plots the average number of replicas
per object and shows how IrisStore gradually regenerates failed
replicas after the failure at time 100.
In particular, the failure affects 2478 objects. Without Paxos
admission-control or Paxos-merging, the regeneration
process does not converge.
Paxos-merging reduces the total number of Paxos invocations from
2478 to 233, while admission-control helps the regeneration
process to converge. Note that the average number of replicas does
not reach 7 even at the end of the experiment because some objects
lose a majority of replicas and cannot regenerate. A single
regeneration takes 21.6sec on average which is dominated by the
time for data transfer (14.3sec) and Paxos (7.3sec). The time for
data transfer is determined by the amount of data and can be much
larger. The convergence time of around 12 minutes is largely
determined by the admission-control parameters and may be tuned to
be faster. However, regeneration is typically not a time-sensitive
task, because IrisStore only needs to finish regeneration before the
next failure hits. Our simulation study based on PL_trace shows
that 12-minute regeneration time achieves almost identical
availability as, say, 5-minute regeneration time. Thus we believe
IrisStore's regeneration mechanism is adequately efficient.
11 Conclusion
Despite the wide awareness of correlated failures in the research
community, the properties of such failures and their impact on system
behavior has been poorly understood. In this
paper, we made some critical steps toward helping system developers
understand the impact of realistic, correlated failures on their
systems. In addition, we provided a set of design principles that
systems should use to tolerate such failures, and showed that some
existing approaches are less effective than one might expect. We presented the
design and implementation of a distributed read/write storage layer,
IrisStore, that uses these design principles to meet availability targets
even under real-world correlated failures.
Acknowledgments. We thank the anonymous reviewers and our
shepherd John Byers for many helpful comments on the paper. We also
thank David Anderson for giving us access to RON_trace, Jay Lorch
for his comments on an earlier draft of the paper, Jeremy Stribling
for explaining several aspects of PL_trace, Hakim
Weatherspoon for providing the code for failure pattern
prediction, Jay Wylie for providing WS_trace, and Praveen
Yalagandula for helping us to process PL_trace. This research was
supported in part by NSF Grant No. CNS-0435382 and funding from
Intel Research.
References
- [1]
-
Akamai Knocked Out, Major Websites Offline.
http://techdirt.com/articles/20040524/0923243.shtml.
- [2]
-
Emulab - network emulation testbed home.
http://www.emulab.net.
- [3]
-
PlanetLab - All Pair Pings.
http://www.pdos.lcs.mit.edu/~strib/pl_app/.
- [4]
-
The MIT RON trace.
David G. Andersen, Private communication.
- [5]
-
Aiyer, A., Alvisi, L., and Bazzi, R.
On the Availability of Non-strict Quorum Systems.
In DISC (2005).
- [6]
-
Bakkaloglu, M., Wylie, J., Wang, C., and Ganger, G.
On Correlated Failures in Survivable Storage Systems.
Tech. Rep. CMU-CS-02-129, Carnegie Mellon University, 2002.
- [7]
-
Barbara, D., and Garcia-Molina, H.
The Reliability of Voting Mechanisms.
IEEE Transactions on Computers 36, 10 (1987).
- [8]
-
Bhagwan, R., Tati, K., Cheng, Y., Savage, S., and Voelker, G. M.
TotalRecall: Systems Support for Automated Availability Management.
In USENIX NSDI (2004).
- [9]
-
Bolosky, W. J., Douceur, J. R., Ely, D., and Theimer, M.
Feasibility of a Serverless Distributed File System Deployed on an
Existing Set of Desktop PCs.
In ACM SIGMETRICS (2000).
- [10]
-
Cates, J.
Robust and Efficient Data Management for a Distributed Hash Table.
Masters Thesis, Massachusetts Institute of Technology, 2003.
- [11]
-
Chun, B., and Vahdat, A.
Workload and Failure Characterization on a Large-Scale Federated
Testbed.
Tech. Rep. IRB-TR-03-040, Intel Research Berkeley, 2003.
- [12]
-
Corbett, P., English, B., Goel, A., Grcanac, T., Kleiman, S., Leong, J.,
and Sankar, S.
Row-Diagonal Parity for Double Disk Failure Correction.
In USENIX FAST (2004).
- [13]
-
Dabek, F., Kaashoek, M. F., Karger, D., Morris, R., and Stoica, I.
Wide-area Cooperative Storage with CFS.
In ACM SOSP (2001).
- [14]
-
Dabek, F., Li, J., Sit, E., Robertson, J., Kaashoek, M. F., and Morris,
R.
Designing a DHT for Low Latency and High Throughput.
In USENIX NSDI (2004).
- [15]
-
Douceur, J. R., and Wattenhofer, R. P.
Competitive Hill-Climbing Strategies for Replica Placement in a
Distributed File System.
In DISC (2001).
- [16]
-
Fried, B. H.
Ex Ante/Ex Post.
Journal of Contemporary Legal Issues 13, 1 (2003).
- [17]
-
Gibbons, P. B., Karp, B., Ke, Y., Nath, S., and Seshan, S.
IrisNet: An Architecture for a Worldwide Sensor Web.
IEEE Pervasive Computing 2, 4 (2003).
- [18]
-
Goodson, G., Wylie, J., Ganger, G., and Reiter, M.
Efficient Byzantine-tolerant Erasure-coded Storage.
In IEEE DSN (2004).
- [19]
-
Haeberlen, A., Mislove, A., and Druschel, P.
Glacier: Highly Durable, Decentralized Storage Despite Massive
Correlated Failures.
In USENIX NSDI (2005).
- [20]
-
Harchol-Balter, M., and Downey, A. B.
Exploiting Process Lifetime Distributions for Dynamic Load
Balancing.
ACM Transactions on Computer Systems 15, 3 (1997).
- [21]
-
Junqueira, F., Bhagwan, R., Hevia, A., Marzullo, K., and Voelker, G.
Surviving Internet Catastrophes.
In USENIX Annual Technical Conference (2005).
- [22]
-
Kubiatowicz, J., Bindel, D., Chen, Y., Czerwinski, S., Eaton, P., Geels,
D., Gummadi, R., Rhea, S., Weatherspoon, H., Weimer, W., Wells, C., and Zhao,
B.
OceanStore: An Architecture for Global-Scale Persistent Storage.
In ACM ASPLOS (2000).
- [23]
-
Lamport, L.
The Part-Time Parliament.
ACM Transactions on Computer Systems 16, 2 (1998).
- [24]
-
Leland, W. E., Taqq, M. S., Willinger, W., and Wilson, D. V.
On the Self-similar Nature of Ethernet Traffic.
In ACM SIGCOMM (1993).
- [25]
-
Lynch, N., and Shvartsman, A.
RAMBO: A Reconfigurable Atomic Memory Service for Dynamic Networks.
In DISC (2002).
- [26]
-
Nath, S.
Exploiting Redundancy for Robust Sensing.
PhD thesis, Carnegie Mellon University, 2005.
Tech. Rep. CMU-CS-05-166.
- [27]
-
Nath, S., Gibbons, P. B., and Seshan, S.
Adaptive Data Placement for Wide-Area Sensing Services.
In USENIX FAST (2005).
- [28]
-
Nath, S., Yu, H., Gibbons, P. B., and Seshan, S.
Tolerating Correlated Failures in Wide-Area Monitoring Services.
Tech. Rep. IRP-TR-04-09, Intel Research Pittsburgh, 2004.
- [29]
-
Nath, S., Yu, H., Gibbons, P. B., and Seshan, S.
Subtleties in Tolerating Correlated Failures in Wide-Area Storage
Systems.
Tech. Rep. IRP-TR-05-52, Intel Research Pittsburgh, 2005.
Also available at http://www.cs.cmu.edu/~yhf/correlated.pdf.
- [30]
-
Nurmi, D., Brevik, J., and Wolski, R.
Modeling Machine Availability in Enterprise and Wide-area
Distributed Computing Environments.
In Euro-Par (2005).
- [31]
-
Plank, J.
A Tutorial on Reed-Solomon Coding for Fault-Tolerance in RAID-like
Systems.
Software – Practice & Experience 27, 9 (1997).
- [32]
-
Rowstron, A., and Druschel, P.
Storage Management and Caching in PAST, A Large-scale, Persistent
Peer-to-peer Storage Utility.
In ACM SOSP (2001).
- [33]
-
Shi, J., and Malik, J.
Normalized Cuts and Image Segmentation.
IEEE Transactions on Pattern Analysis and Machine Intelligence
22, 8 (2000).
- [34]
-
Tang, D., and Iyer, R. K.
Analysis and Modeling of Correlated Failures in Multicomputer
Systems.
IEEE Transactions on Computers 41, 5 (1992).
- [35]
-
Thomas, R. H.
A Majority Consensus Approach to Concurrency Control for Multiple
Copy Databases.
ACM Transactions on Database Systems 4, 2 (1979).
- [36]
-
Weatherspoon, H., Chun, B.-G., So, C. W., and Kubiatowicz, J.
Long-Term Data Maintenance: A Quantitative Approach.
Tech. Rep. UCB/CSD-05-1404, University of California, Berkeley, 2005.
- [37]
-
Weatherspoon, H., Moscovitz, T., and Kubiatowicz, J.
Introspective Failure Analysis: Avoiding Correlated Failures in
Peer-to-Peer Systems.
In IEEE RPPDS (2002).
- [38]
-
Yalagandula, P., Nath, S., Yu, H., Gibbons, P. B., and Seshan, S.
Beyond Availability: Towards a Deeper Understanding of Machine
Failure Characteristics in Large Distributed Systems.
In USENIX WORLDS (2004).
- [39]
-
Yu, H.
Overcoming the Majority Barrier in Large-Scale Systems.
In DISC (2003).
- [40]
-
Yu, H.
Signed Quorum Systems.
In ACM PODC (2004).
- [41]
-
Yu, H., and Vahdat, A.
Consistent and Automatic Replica Regeneration.
ACM Transactions on Storage 1, 1 (2005).
- 1
- Work done while this author was a graduate student at CMU and an intern at Intel
Research Pittsburgh.
- 2
- Note that PL_trace
has sporadic “gaps”, see [29] for how we
classify the gaps and treat them properly based on their causes.
- 3
- This
threshold is the smallest to provide a plausible number of
near-source partitions. Using a smaller threshold would imply that
the client (on Internet2) experiences a near-source partition >
4% of the time in our trace, which is rather unlikely.
- 4
- The trace actually contains 1909 web servers, but
the authors analyzed only 306 servers because those are the only
ones that ever failed during the four weeks.
- 5
- Crashing random sets of
nodes is our explicit choice for the experimental setup. The reason
is exactly the same as in our bi-exponential failure correlation
model (see Section 4).
- 6
- Note that the y-axis is on
log-scale, and that is why the summation of two straight lines does
not result in a third straight line.
- 7
- The same
conclusion also holds if we directly use WS_trace to drive the simulation.
- 8
- http://www.intel-iris.net/irislog
- 9
- RAMBO has never been deployed over the
wide-area, while Om has never been evaluated under a large number of
simultaneous node failures.
This document was translated from LATEX by
HEVEA.
|