Efficient Replica Maintenance for Distributed Storage Systems

This paper considers replication strategies for storage systems that aggregate the disks of many nodes spread over the Internet. Maintaining replication in such systems can be prohibitively expensive, since every transient network or host failure could potentially lead to copying a server's worth of data over the Internet to maintain replication levels.

The following insights in designing an efficient replication algorithm emerge from the paper's analysis. First, durability can be provided separately from availability; the former is less expensive to ensure and a more useful goal for many wide-area applications. Second, the focus of a durability algorithm must be to create new copies of data objects faster than permanent disk failures destroy the objects; careful choice of policies for what nodes should hold what data can decrease repair time. Third, increasing the number of replicas of each data object does not help a system tolerate a higher disk failure probability, but does help tolerate bursts of failures. Finally, ensuring that the system makes use of replicas that recover after temporary failure is critical to efficiency.

Based on these insights, the paper proposes the Carbonite replication algorithm for keeping data durable at a low cost. A simulation of Carbonite storing 1 TB of data over a 365 day trace of PlanetLab activity shows that Carbonite is able to keep all data durable and uses 44% more network traffic than a hypothetical system that only responds to permanent failures. In comparison, Total Recall and DHash require almost a factor of two more network traffic than this hypothetical system.

1  Introduction

The threat to durability is losing the last copy of an object due to permanent failures of disks. Efficiently countering this threat to durability involves three main challenges. First, network bandwidth is a scarce resource in a wide-area distributed storage system. To store objects durably, there must be enough network capacity to create copies of objects faster than they are lost due to disk failure. Second, a system cannot always distinguish between transient failures and permanent disk failures: it may waste network bandwidth by creating new copies during transient failures. Third, after recovery from transient failures, some replicas may be on nodes that the replica lookup algorithm does not query and are thus effectively lost.

Since transient failures are common in wide-area systems, replication algorithms can waste bandwidth by making unneeded replicas. For example, the initial replication algorithm [6] that the DHash distributed hash table (DHT) [9] turned out to be inadequate to build storage applications such as UsenetDHT [34], Antiquity [11], and OverCite [35, 36].

A problem with DHash was that its design was driven by the goal of achieving 100% availability; this decision caused it to waste bandwidth by creating new replicas in response to temporary failures. Its design and similar ones (such as Total Recall [3]) are overkill for durability. Furthermore, users of many Internet applications can tolerate some unavailability. For example, Usenet readers will see all articles eventually, as long as they are stored durably. Our experience with these DHT applications has led us to the following insights:

• Durability is a more practical and useful goal than availability for applications that store objects (as opposed to caching objects).
• The main goal of a durability algorithm should be to create new copies of an object faster than they are destroyed by disk failures; the choice of how replicas are distributed among nodes can make this task easier.
• Increasing the replication level does not help tolerate a higher average permanent failure rate, but it does help cope with bursts of failures.
• Reintegrating returning replicas is key to avoiding unnecessary copying.

Carbonite's design assumes that the disks in the distributed storage system fail independently of each other: failures of geographically distributed hard drives from different manufacturers are likely to be uncorrelated.

In a year-long PlanetLab failure trace, however, we observe some correlated failures because of coordinated re-installs of the PlanetLab software. Despite this, an evaluation using the PlanetLab failure trace shows that Carbonite is able to keep 1 TB of data durable, and consumes only 44% more network traffic than a hypothetical system that only responds to permanent failures. In comparison, Total Recall and DHash require almost a factor of two more network traffic than this hypothetical system.

The rest of this paper explains our durability models and algorithms, interleaving evaluation results into the explanation. Section 2 describes the simulated evaluation environment. Section 3 presents a model of the relationship between network capacity, amount of replicated data, number of replicas, and durability. Section 4 explains how to decrease repair time, and thus increase durability, by proper placement of replicas on servers. Section 5 presents an algorithm that reduces the bandwidth wasted making copies due to transient failures. Section 6 outlines some of the challenges that face practical implementations of these ideas, Section 7 discusses related work, and Section 8 concludes.

2  System environment

2.1  PlanetLab characteristics

The main characteristics of PlanetLab that interest us are the rates of disk and transient failures. We use historical data collected by the CoMon project [25] to identify transient failures. CoMon has archival records collected on average every 5 minutes that include the uptime as reported by the system uptime counter on each node. We use resets of this counter to detect reboots, and we estimate the time when the node became unreachable based on the last time CoMon was able to successfully contact the node. This allows us to pinpoint failures without depending on the reachability of the node from the CoMon monitoring site.

We define a disk failure to be any permanent loss of disk contents, due to disk hardware failure or because its contents are erased accidentally or intentionally. In order to identify disk failures, the CoMon measurements were supplemented with event logs from PlanetLab Central [28]. This database automatically records each time a PlanetLab node is reinstalled (e.g., for an upgrade, or after a disk is replaced following a failure). The machine is then considered offline until the machine is assigned a regular boot state in the database. Table 1 summarizes the statistics of this trace. Figure 7(a) visualizes how transient and disk failures accumulate over time in this network.

---

Dates	1 March 2005 – 28 Feb 2006
Number of hosts	632
Number of transient failures	21255
Number of disk failures	219
Transient host downtime (s)	1208, 104647, 14242
Any failure interarrival (s)	305, 1467, 3306
Disk failures interarrival (s)	54411, 143476, 490047
(Median/Mean/90th percentile)

Table 1: CoMon+PLC trace characteristics.

---

2.2  Synthetic trace

Each synthetic trace contains 632 nodes, just like the PlanetLab trace. The mean session time and downtime match the values shown in Table 1; however, in order to increase the failure density, we extended the length to two years and reduced the average node lifetime to one year. Each experiment was run with ten different traces; the figures show the averages from these experiments.

2.3  Simulation

The simulator takes as input a trace of transient and disk failure events, node repairs and object insertions. It simulates the behavior of nodes under different protocols and produces a trace of the availability of objects and the amount of data sent and stored by each node for each hour of simulated time. Each simulation calls put with 50,000 data objects, each of size 20 MB. Unless otherwise noted, each node is configured with an access link capacity of 150 KBytes/s, roughly corresponding to the throughput achievable under the bandwidth cap imposed by PlanetLab. The goal of the simulations is to show the percentage of objects lost and the amount of bandwidth needed to sustain objects over time.

3  Understanding durability

3.1  Challenges to durability

In order to handle some average rate of failure, a high-durability system must have the ability to create new replicas of objects faster than replicas are destroyed. Whether the system can do so depends on the per-node network access link speed, the number of nodes (and hence access links) that help perform each repair, and the amount of data stored on each failed node. When a node n fails, the other nodes holding replicas of the objects stored on n must generate replacements: objects will remain durable if there is sufficient bandwidth available on average for the lost replicas to be recreated. For example, in a symmetric system each node must have sufficient bandwidth to copy the equivalent of all data it stores to other nodes during its lifetime.

If nodes are unable to keep pace with the average failure rate, no replication policy can prevent objects from being lost. These systems are infeasible. If the system is infeasible, it will eventually “adapt” to the failure rate by discarding objects until it becomes feasible to store the remaining amount of data. A system designer may not have control over access link speeds and the amount of data to be stored; fortunately, choice of object placement can improve the speed that a system can create new replicas as discussed in Section 4.

If the creation rate is only slightly above the average failure rate, then a burst of failures may destroy all of an object's replicas before a new replica can be made; a subsequent lull in failures below the average rate will not help replace replicas if no replicas remain. For our purposes, these failures are simultaneous: they occur closer together in time than the time required to create new replicas of the data that was stored on the failed disk. Simultaneous failures pose a constraint tighter than just meeting the average failure rate: every object must have more replicas than the largest expected burst of failures. We study systems that aim to maintain a target number of replicas in order to survive bursts of failure; we call this target r_L.

Higher values of r_L do not allow the system to survive a higher average failure rate. For examples, if failures were to arrive at fixed intervals, then either r_L=2 would always be sufficient, or no amount of replication would ensure durability. If r_L = 2 is sufficient, there will always be time to create a new replica of the objects on the most recently failed disk before their remaining replicas fail. If creating new replicas takes longer than the average time between failures, no fixed replication level will make the system feasible; setting a replication level higher than two would only increase the number of bytes each node must copy in response to failures, which is already infeasible at r_L=2.

3.2  Creation versus failure rate

---

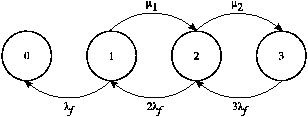
Figure 1: A continuous time Markov model for the process of replica failure and repair for a system that maintains three replicas (r_L=3). Numbered states correspond to the number of replicas of each object that are durable. Transitions to the left occur at the rate at which replicas are lost; right-moving transitions happen at the replica creation rate.

---

This model can be analyzed numerically to shed light on the impact of r_L on the probability of data loss; we will show this in Section 3.3. However, to gain some intuition about the relationship between creation and failure rates and the impact this has on the number of replicas that can be supported, we consider a simplification of Figure 1 that uses a fixed μ but repairs constantly, even allowing for transitions out of state 0. While these changes make the model less realistic, they turn the model into an M/M/∞ queue [19] where the “arrival rate” is the repair rate and the “service rate” is the per-replica failure rate. The “number of busy servers” is the number of replicas: the more replicas an object has, the more probable it is that one of them will fail.

This simplification allows us to estimate the equilibrium number of replicas: it is μ/λ_f. Given μ and λ_f, a system cannot expect to support more than this number of replicas. For example, if the system must handle coincidental bursts of five failures, it must be able to support at least six replicas and hence the replica creation rate must be at least 6 times higher than the average replica failure rate. We will refer to μ/λ_f as θ. Choices for r_L are effectively limited by θ. It is not the case that durability increases continuously with r_L; rather, when using r_L > θ, the system provides the best durability it can, given its resource constraints. Higher values of θ decrease the time it takes to repair an object, and thus the `window of vulnerability' during which additional failures can cause the object to be destroyed.

To get an idea of a real-world value of θ, we estimate μ and λ_f from the historical failure record for disks on PlanetLab. From Table 1, the average disk failure inter-arrival time for the entire test bed is 39.85 hours. On average, there were 490 nodes in the system, so we can estimate the mean time between failures for a single disk as 490⋅ 39.85 hours or 2.23 years. This translates to λ_f ≈ 0.439 disk failures per year.

The replica creation rate μ depends on the achievable network throughput per node, as well as the amount of data that each node has to store (including replication). PlanetLab currently limits the available network bandwidth to 150 KB/s per node, and if we assume that the system stores 500 GB of unique data per node with r_L = 3 replicas each, then each of the 490 nodes stores 1.5 TB. This means that one node's data can be recreated in 121 days, or approximately three times per year. This yields μ ≈ 3 disk copies per year.

In a system with these characteristics, we can estimate θ = μ/λ_f ≈ 6.85, though the actual value is likely to be lower. Note that this ratio represents the equilibrium number of disks worth of data that can be supported; if a disk is lost, all replicas on that disk are lost. When viewed in terms of disk failures and copies, θ depends on the value of r_L: as r_Lincreases, the total amount of data stored per disk (assuming available capacity) increases proportionally and reduces μ. If λ_f = μ, the system can in fact maintain r_Lreplicas of each object.

To show the impact of θ, we ran an experiment with the synthetic trace (i.e., with 632 nodes, a failure rate of λ_f = 1 per year and a storage load of 1 TB), varying the available bandwidth per node. In this case, 100 B/s corresponds to θ=1.81 / r_L. Figure 2 shows that, as θ drops below one, the system can no longer maintain full replication and starts operating in a `best effort' mode, where higher values of r_L do not give any benefit. The exception is if some of the initial r_L replicas survive through the entire trace, which explains the small differences on the left side of the graph.

---

Figure 2: Average number of replicas per object at the end of a two-year synthetic trace for varying values of θ, which varies with bandwidth per node (on the x-axis) and total data stored (r_L). Where θ < 1, the system cannot maintain the full replication level; increasing r_L further does not have any effect.

---

3.3  Choosing r_L

---

Figure 3: Frequency of “simultaneous” failures in the PlanetLab trace. These counts are derived from breaking the trace into non-overlapping 24 and 72 hour periods and noting the number of permanent failures that occur in each period. If there are x replicas of an object, there were y chances in the trace for the object to be lost; this would happen if the remaining replicas were not able to respond quickly enough to create new replicas of the object.

---

One approach is to set r_Lto one more than the maximum burst of simultaneous failures in a trace of a real system. For example, Figure 3 shows the burstiness of permanent failures in the PlanetLab trace by counting the number of times that a given number of failures occurs in disjoint 24 hour and 72 hour periods. If the size of a failure burst exceeds the number of replicas, some objects may be lost. From this, one might conclude that 12 replicas are needed to maintain the desired durability. This value would likely provide durability but at a high cost. If a lower value of r_Lwould suffice, the bandwidth spent maintaining the extra replicas would be wasted.

There are several factors to consider in choosing r_Lto provide a certain level of durability. First, even if failures are independent, there is a non-zero (though small) probability for every burst size up to the total number of nodes. Second, a burst may arrive while there are fewer than r_Lreplicas. One could conclude from these properties that the highest possible value of r_Lis desirable. On the other hand, the simultaneous failure of even a large fraction of nodes may not destroy any objects, depending on how the system places replicas (see Section 4). Also, the workload may change over time, affecting μ and thus θ.

The continuous time Markov model described in Figure 1 reflects the distributions of both burst size and object replication level. The effect of these distributions is significant. An analysis of the governing differential equations can be used to derive the probability that an object will be at a given replication level after a given amount of time. In particular, we can determine the probability that the chain is in state 0, corresponding to a loss of durability.

We show the results of such an analysis in Figure 4; for details, see [7]. To explore different workloads, we consider different amounts of data per node. The graph shows the probability that an object will survive after four years as a function of r_L and data stored per node (which affects the repair rate and hence θ).

As r_L increases, the system can tolerate more simultaneous failures and objects are more likely to survive. The probability of object loss at r_L=1 corresponds to using no replication. This value is the same for all curves since it depends only on the lifetime of a disk; no new replicas can be created once the only replica of the object is lost. To store 50 GB durably, the system must use an r_L of at least 3. As the total amount of data increases, the r_L required to attain a given survival probability also increases. Experiments confirm that data is lost on the PlanetLab trace only when maintaining fewer than three replicas.

---

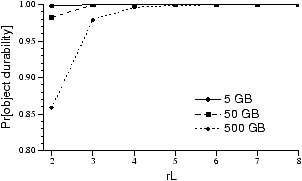
Figure 4: Analytic prediction for object durability after four years on PlanetLab. The x-axis shows the initial number of replicas for each object: as the number of replicas is increased, object durability also increases. Each curve plots a different per-node storage load; as load increases, it takes longer to copy objects after a failure and it is more likely that objects will be lost due to simultaneous failures.

---

4  Improving repair time

Each node, n, designates a set of other nodes that can potentially hold copies of the objects that n is responsible for. We will call the size of that set the node's scope, and consider only system designs in which every node has the same scope. Scope can range from a minimum of r_L to a maximum of the number of nodes in the system.

A small scope means that all the objects stored on node n have copies on nodes chosen from the same restricted set of other nodes. The advantage of a small scope is that it makes it easier to keep track of the copies of each object. For example, DHash stores the copies of all the objects with keys in a particular range on the successor nodes of that key range; the result is that those nodes store similar sets of objects, and can exchange compressed summaries of the objects they store when they want to check that each object is replicated a sufficient number of times [6].

The disadvantage of a small scope is that the effort of creating new copies of objects stored on a failed disk falls on the small set of nodes in that disk's scope. The time required to create the new copies is proportional to the amount of data on one disk divided by the scope. Thus a small scope results in a long recovery time. Another problem with a small scope, when coupled with consistent hashing, is that the addition of a new node may cause needless copying of objects: the small scope may dictate that the new node replicate certain objects, forcing the previous replicas out of scope and thus preventing them from contributing to durability.

Larger scopes spread the work of making new copies of objects on a failed disk over more access links, so that the copying can be completed faster. In the extreme of a scope of N (the number of nodes in the system), the remaining copies of the objects on a failed disk would be spread over all nodes, assuming that there are many more objects than nodes. Furthermore, the new object copies created after the failure would also be spread over all the nodes. Thus the network traffic sources and destinations are spread over all the access links, and the time to recover from the failure is short (proportional to the amount of data on one disk divided by N).

A larger scope also means that a temporary failure will be noticed by a larger number of nodes. Thus, more access links are available to create additional replicas while the failure lasts. Unless these links are already fully utilized, this increases the effective replica creation rate, and thus improves durability.

---

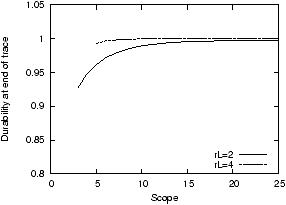
Figure 5: Durability for different scopes in a synthetic trace with low θ. Larger scopes spread the repair work over more access links and improve the nodes' ability to monitor replicas and temporary failures, which results in higher durability.

---

A large scope reduces repair time and increases durability; however, implementing a large scope presents two trade-offs. First, the system must monitor each node in the scope to determine the replication levels; when using a large scope, the system must monitor many nodes. This increased monitoring traffic limits scalability. Second, in some instances, a large scope can increase the likelihood that a simultaneous failure of multiple disks will cause some object to be lost.

If objects are placed randomly with scope N and there are many objects, then it is likely that all _NC_rL potential replica sets are used. In this scenario, the simultaneous failure of any r_L disks is likely to cause data loss: there is likely to be at least one object replicated on exactly those disks. A small scope limits placement possibilities that are used, concentrating objects into common replica sets. As a result, it is less likely that a given set of r_L failures will affect a replica set, but when data loss does occur, many more objects will be lost. These effects exactly balance: the expected number of objects lost during a large failure event is identical for both strategies. It is the variance that differs between the two strategies.

5  Reducing transient costs

The key technique needed to achieve this is to ensure that the system reintegrates object replicas stored on nodes after transient failures; this means the system must be able to track more than r_L replicas of each object. The number of replicas that the system must remember turns out to be dependent on a, the average fraction of time that a node is available. However, we show that the correct number of extra replicas can be determined without estimating a by tracking the location of all replicas, including those that are offline. We introduce the Carbonite algorithm that uses this technique and demonstrate its effectiveness using simulations.

We additionally consider two other techniques for limiting response to transient failures: creating extra replicas in batches and using timeouts as a heuristic for distinguishing transient from disk failures. Both are of limited value: batching is best able to save bandwidth when using erasure codes and, in the presence of reintegration, timeouts work well only if node downtimes are notably shorter than node (and disk) lifetimes.

5.1  Carbonite details

Because it is not possible to distinguish between transient and disk failures remotely, Carbonite simply responds to any detected failure by creating a new replica. This approach is shown in Figure 6. If fewer than r_L replicas are detected as available, the algorithm creates enough new replicas to return the replication level to r_L.

---

// Iterate through the object database
// and schedule an object for repair if needed
Maintain_Replicas ()
    keys = <DB.object_keys sorted number of available replicas>
    foreach k in keys:
	n = replicas[k].len ()
	if n < rL:
	    newreplica = enqueue_repair (k)
	    replicas[k].append (newreplica)

Figure 6: Each node maintains a list of objects for which it is responsible and monitors the replication level of each object using some synchronization mechanism. In this code, this state is stored in the replicas hash table though an implementation may choose to store it on disk. This code is called periodically to enqueue repairs on those objects that have too few replicas available; the application can issue these requests at its convenience.

---

5.2  Reintegration reduces maintenance

---

(a)	(b)

Figure 7: A comparison of the total amount of work done by different maintenance algorithms with r_L=3 using a PlanetLab trace (left) and a synthetic trace (right). In all cases, no objects are lost. However, r_L = 2 is insufficient: for the PlanetLab trace, even a system that could distinguish permanent from transient failures would lose several objects.

---

Unlike all other synthetic traces used in this paper, whose parameters are different from the PlanetLab trace in order to bring out the basic underlying trends, the synthetic trace used in Figure 7 was configured to be similar to the PlanetLab trace. In particular, the average node lifetime and the median downtime are the same. The result is still an approximation (for example, PlanetLab grew during the trace) but the observed performance is similar. Some of the observed differences are due to batching (used by Total Recall) and timeouts (used by all systems); the impact of these are discussed in more detail in Sections 5.4 and 5.5.

Since the oracle system responds only to disk failures, it uses the lowest amount of bandwidth. The line labeled Cates shows a system that keeps track of exactly r_L replicas per object; this system approximates the behavior of DHTs like DHash, PAST and OpenDHT. Each failure causes the number of replicas to drop below r_L and causes this system to create a new copy of an object, even if the failure was transient. If the replica comes back online, it is discarded. This behavior results in the highest traffic rate shown. The difference in performance between the PlanetLab and Poisson trace is due to differences in the distribution of downtimes: Poisson is not a particularly good fit for the PlanetLab downtime distribution.

Total Recall [3] tracks up to a fixed number of replicas, controlled by a parameter r_H; we show r_H = 5 which is optimal for these traces, and r_H = 9. As can be seen at the right of the graphs, this tracking of additional replicas allows Total Recall to create fewer replicas than the Cates system. When more than r_L replicas are available, a transient failure will not cause Total Recall to make a new copy. However, Total Recall's performance is very sensitive to r_H. If r_H is set too low, a series of transient failures will cause the replication level to drop below r_L and force it to create an unnecessary copy. This will cause Total Recall to approach Cates (when r_H = r_L). Worse, when the system creates new copies it forgets about any copies that are currently on failed nodes and cannot benefit from the return of those copies. Without a sufficiently long memory, Total Recall must make additional replicas. Setting r_Htoo high imposes a very high insertion cost and results in work that may not be needed for a long time.

Carbonite reintegrates all returning replicas into the replica sets and therefore creates fewer copies than Total Recall. However, Carbonite's inability to distinguish between transient and disk failures means that it produces and maintains more copies than the oracle based algorithm. This is mainly visible in the first weeks of the trace as Carbonite builds up a buffer of extra copies. By the end of the simulations, the rate at which Carbonite produces new replicas approaches that of the oracle system.

5.3  How many replicas?

By computing the Chernoff bound, it is possible to show that after the system has created 2r_L/a replicas, the probability of a new object creation is exponentially small. 2r_L/a is a rough (and somewhat arbitrary) estimate of when the probability of a new object creation is small enough to ignore. Figure 8 shows (on the y-axis) the probability that a new object must be created when an increasing number of replicas already exist. As r increases, the probability that a new replica needs to be created falls, and the algorithm creates replicas less frequently. As r approaches 2r_L/a, the algorithm essentially stops creating replicas, despite not knowing the value of a.

---

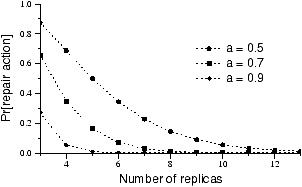
Figure 8: Additional redundancy must be created when the amount of live redundancy drops below the desired amount (3 replicas in this example). The probability of this happening depends solely on the average node availability a and the amount of durable redundancy. This graph shows the probability of a repair action as a function of the amount of durable redundancy, with a = 0.5, a = 0.7 and a = 0.9 for a replication system.

---

5.4  Create replicas as needed

Another idea is to create not only enough copies to bring the number of available replicas back up to r_L, but also e additional copies beyond r_L (this is similar to Total Recall's lazy repair technique). Creating a batch of copies makes repair actions less frequent, but at the same time, causes more maintenance traffic than Carbonite. The work required to create additional replicas will be wasted if those replicas are lost due to disk failures before they are actually required. Carbonite, on the other hand, only creates replicas that are necessary to keep r_L replicas available. In other words, either Carbonite would eventually create the same number of replicas as a scheme that creates replicas in batches, or some replicas created in the batch were unnecessary: batch schemes do, at best, the same amount of work as Carbonite.

---

Figure 9: Total repair cost with extra replicas, and with and without reintegration after repair. Without reintegration, extra replicas reduce the rate at which repair is triggered and thus reduce maintenance cost; there is an optimal setting (here e=8). With reintegration, the cost is lowest if no extra replicas are used.

---

In the scenario without reintegration, replicas that are unavailable when repair is triggered are not reintegrated into the replica set even if they do return. Total Recall behaves this way. Extra replicas give the system a short-term memory. Additional replicas increase the time until repair must be made (at which time failed replicas will be forgotten); during this time failed replicas can be reintegrated. Larger values of e give the system a longer memory but also put more data at risk of failure: on this synthetic trace, a value of e=8 is optimal. Taking advantage of returning replicas is simpler and more efficient than creating additional replicas: a system that reintegrates returning replicas will always make fewer copies than a system that does not and must replace forgotten replicas.

For systems that use erasure codes, there is an additional read cost since a complete copy of the object is needed in order to generate a new fragment [32]. The cost of reading a sufficient number of fragments prior to recreating a lost fragment can overwhelm the savings that erasure codes provide. A common approach is to amortize this cost by batching fragment creation but simply caching the object at the node responsible for repair is much more effective. A simulation contrasting both caching and batching (but both with reintegration) shows results similar to Figure 9: caching the object with a 7/14 erasure code uses 85% of the bandwidth that the optimal batching strategy would use.

5.5  Timeouts

The goal of both reintegrating replicas and use of timeouts is to reduce the number of repairs without decreasing durability. Figure 7 demonstrates that reintegration is effective for Carbonite. However, it also illustrates that timeouts are important in systems without reintegration: on the PlanetLab trace, the timeout used is able to mask 87.7% of transient failures whereas it only masks 58.3% of transient failures on the Poisson trace. If replicas are reintegrated, what extra benefit does a timeout provide?

Timeouts are most effective when a significant percentage of the transient failures can be ignored, which is dependent on the downtime distribution. However, for durability to remain high, the expected node lifetime needs to be significantly greater than the timeout.

---

[] []

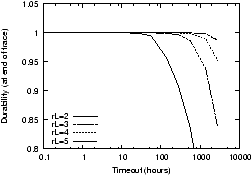
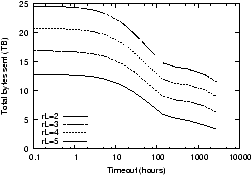
Figure 10: The impact of timeouts on bandwidth and durability on a synthetic trace. Figure 10(a) shows the number of copies created for various timeout values; fig10b shows the corresponding object durability. In this trace, the expected downtime is about 29 hours. Longer timeouts allow the system to mask more transient failures and thus reduce maintenance cost; however, they also reduce durability.

---

Figure 10 shows the results of this simulation: fig10a shows the total bytes sent as a function of timeout while fig10b shows the durability at the end of the trace. As the length of the timeout increases past the average downtime, we observe a reduction in the number of bytes sent without a decrease in durability. However, as the timeout grows longer, durability begins to fall: the long timeout delays the point at which the system can begin repair, reducing the effective repair rate. Thus setting a timeout can reduce response to transient failures but its success depends greatly on its relationship to the downtime distribution and can in some instances reduce durability as well.

6  Implementing Carbonite

In a DHT, each node is algorithmically assigned a portion of the total identifier space that it is responsible for maintaining. Carbonite requires that each node know the number of available replicas of each object for which it is responsible. The goal of monitoring is to allow the nodes to track the number of available replicas and to learn of objects that the node should be tracking but is not aware of. When a node n fails the new node n' that assumes responsibility of n's blocks begins tracking replica availability; monitored information is soft state and thus can be failed over to a "successor" relatively transparently.

Monitoring can be expensive: a node might have to contact every node in the scope of each object it holds. While developing two prototype implementations of Carbonite in the PlanetLab environment, we found it necessary to develop different techniques for monitoring: the monitoring problem is slightly different in systems that use distributed directories and those that use consistent hashing. Figure 11 illustrates the structures of these systems.

---

[DHT] 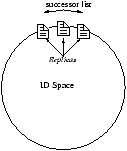  [Directory]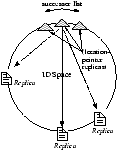

Figure 11: DHT- and Directory- Based Storage System Architectures.

---

We used Oceanstore [20, 30] and the BambooDHT [31] to develop a distributed directory system using large scope and random placement. Oceanstore must maintain pointers to all nodes that have ever held data for a given object and has a scope of N. Responsibility for keys is still assigned using consistent hashing: the pointer database for each key is replicated on the successors of the key. In this case, the location of objects is hard state. Unfortunately, it could be easy for this system to have very high monitoring costs: if each node communicate with every other node periodically, the resulting N² probe traffic may limit the system's scalability.

6.1  Monitoring consistent hashing systems

DHash uses a synchronization protocol based on Merkle trees [6] that takes advantage of the fact that most objects are typically correctly placed. In this common case, adjacent nodes store largely similar keys and two nodes can exchange a single message (containing a digest of the stored keys) to verify that they are synchronized.

Carbonite allows replicas to be placed anywhere in the placement scope. This flexibility lets the system avoid moving and replicating objects during most joins (until the system grows dramatically). However, it also causes the Merkle synchronization protocol to operate outside of its common case: adjacent nodes are no longer likely to store nearly identical sets of objects. In this environment the synchronizer “discovers” that nodes in the scope are missing objects each time it is run. Repeatedly exchanging this information can be costly: if the synchronization protocol runs once a minute, the cost of repeatedly transferring the 20-byte key of an 8 KB data object will exceed the cost of transferring the object itself to a newly joined node in about 8 hours.

To avoid this problem, each node maintains, for each object, a list of nodes in the scope without a copy of the object. The node uses this information to adjust its Merkle tree to avoid re-learning the information again during the next run of the synchronizer. For instance, when a node n synchronizes with a replica node n' that is known to be missing an object with key k, n leaves k out of the Merkle tree used for synchronization: this prevents n' from reporting what n already knew. The amount of extra state needed to perform this optimization per object is small relative to the size of storing the object itself, and can be maintained lazily, unlike the object itself which is hard state.

6.2  Monitoring host availability

The DHT's routing tables are used to establish a unique spanning tree rooted at each node a O(logN) out-degree per node. Each node periodically broadcasts a heartbeat message to its children in the tree; this message includes a generation identifier that is randomly generated when the node is installed or reinstalled following a disk failure. The children rebroadcast the heartbeat to their children until it is received by all nodes.

Over time, each node expects to receive regular notification of node liveness. If a heartbeat is missed, the monitoring node triggers repair for every object stored on the newly down node. When a node returns and its generation identifier has not changed, the monitoring node can conclude that objects stored on that node are again accessible.

7  Related work

7.1  Replication analysis

The model and discussion in this paper is similar to contemporary work that looks at churn [37] and analyzes the expected object lifetime [29]. The birth-death model is a generalization of the calculations that predict the MTBF for RAID storage systems [26]. Owing to its scale, a distributed system has more flexibility to choose parameters such as the replication level and number of replica sets when compared to RAID systems.

Blake and Rodrigues argue that wide-area storage systems built on unreliable nodes cannot store a large amount of data [4]. Their analysis is based on the amount of data that a host can copy during its lifetime and mirrors our discussion of feasibility. We come to a different conclusion because we consider a relatively stable system membership where data loss is driven by disk failure, while they assumed a system with continual membership turnover.

The selection of a target replication level for surviving bursts differs from many traditional fault tolerant storage systems. Such systems, designed for single-site clusters, typically aim to continue operating despite some fixed number of failures and choose number of replicas so that a voting algorithm can ensure correct updates in the presence of partitions or Byzantine failures [23, 5, 17, 33, 24].

FAB [33] and Chain Replication [38] both consider how the number of possible replicas sets affects data durability. The two come to opposite conclusions: FAB recommends a small number of replica sets since more replica sets provide more ways for data to fail; chain replication recommends many replica sets to increase repair parallelism and thus reduce repair time. These observations are both correct: choosing a replica placement strategy requires balancing the probability of losing some data item during a simultaneous failure (by limiting the number of replica sets) and improving the ability of the system to tolerate a higher average failure rate (by increasing the number of replica sets and reconstruction parallelism).

Weatherspoon et al [39] studied the increased costs due to transient failures. Their results quantify the benefits of maintaining extra replicas in reducing these transient costs. However, their analysis focuses on systems that forget about extant replicas that exist when repair is initiated and do not discuss the benefits of reintegrating them.

7.2  Replicated systems

Distributed databases [10], online disaster recovery systems such as Myriad [22], and storage systems [13, 12, 27] use replication and mirroring to distribute load and increase durability. These systems store mutable data and focus on the cost of propagating updates, a consideration not applicable to the immutable data we assume. In some cases, data is replicated between a primary and backup sites and further replicated locally at each site using RAID. Wide area recovery is initiated only after site failure; individual disk failure can be repaired locally.

Total Recall is the system most similar to our work [3]. We borrow from Total Recall the idea that creating and tracking additional replicas can reduce the cost of transient failures. Total Recall's lazy replication keeps a fixed number of replicas and fails to reincorporate replicas that return after a transient failure if a repair had been performed. Total Recall also requires introspection or guessing to determine an appropriate high water mark that Carbonite can arrive at naturally.

Glacier [18] is a distributed storage system that uses massive replication to provide data durability across large-scale correlated failure events. The resulting tradeoffs are quite different from those of Carbonite, which is designed to handle a continuous stream of at small-scale failure events. For example, due to its high replication level, Glacier can afford very long timeouts and thus mask almost all transient failures.

8  Conclusions and future work

These techniques have allowed us to develop and deploy prototypes of UsenetDHT [34], OverCite [35], and Antiquity [11]. These systems must store large amounts of data durably and were infeasible without the techniques we have presented. In the future, we hope to report on our long-term experience with these systems.

Acknowledgments

References

[1]

Andersen, D. Improving End-to-End Availability Using Overlay Networks. PhD thesis, Massachusetts Institute of Technology, 2004.

[2]

Anderson, T. E., Dahlin, M. D., Neefe, J. M., Patterson, D. A., Roselli, D. S., and Wang, R. Y. Serverless network file systems. In Proc. of the 15th ACM Symposium on Operating System Principles (Dec. 1995).

[3]

Bhagwan, R., Tati, K., Cheng, Y.-C., Savage, S., and Voelker, G. M. Total Recall: System support for automated availability management. In Proc. of the 1st Symposium on Networked Systems Design and Implementation (Mar. 2004).

[4]

Blake, C., and Rodrigues, R. High availability, scalable storage, dynamic peer networks: Pick two. In Proc. of the 9th Workshop on Hot Topics in Operating Systems (May 2003), pp. 1–6.

[5]

Castro, M., and Liskov, B. Practical byzantine fault tolerance and proactive recovery. ACM Transactions on Computer Systems 20, 4 (2002), 398–461.

[6]

Cates, J. Robust and efficient data management for a distributed hash table. Master's thesis, Massachusetts Institute of Technology, May 2003.

[7]

Dabek, F. A Distributed Hash Table. PhD thesis, Massachusetts Institute of Technology, 2005.

[8]

Dabek, F., Kaashoek, M. F., Karger, D., Morris, R., and Stoica, I. Wide-area cooperative storage with CFS. In Proc. of the 18th ACM Symposium on Operating System Principles (Oct. 2001).

[9]

Dabek, F., Li, J., Sit, E., Robertson, J., Kaashoek, M. F., and Morris, R. Designing a DHT for low latency and high throughput. In Proc. of the 1st Symposium on Networked Systems Design and Implementation (Mar. 2004).

[10]

Demers, A., Greene, D., Hauser, C., Irish, W., Larson, J., Shenker, S., Sturgis, H., Swinehart, D., and Terry, D. Epidemic algorithms for replicated database maintenance. In Proc. of the 6th ACM Symposium on Principles of Distributed Computing (1987), pp. 1–12.

[11]

Eaton, P., Weatherspoon, H., and Kubiatowicz, J. Efficiently binding data to owners in distributed content-addressable storage systems. In Proc. of the 3rd International Security in Storage Workshop (Dec. 2005).

[12]

EMC. Centera—content addressed storage system. https://www.emc.com/products/systems/centera.jsp. Last accessed March 2006.

[13]

EMC. Symmetrix remote data facility. https://www.emc.com/products/networking/srdf.jsp. Last accessed March 2006.

[14]

Freedman, M. J., Lakshminarayanan, K., Rhea, S., and Stoica, I. Non-transitive connectivity and DHTs. In Proc. of the 2nd Workshop on Real Large Distributed Systems (Dec. 2005).

[15]

Ghemawat, S., Gobioff, H., and Leung, S.-T. The Google file system. In Proc. of the 2003 19th ACM Symposium on Operating System Principles (Oct. 2003).

[16]

Gray, J., McJones, P., Blasgen, M., Lindsay, B., Lorie, R., Price, T., Putzolu, F., and Traiger, I. The recovery manager of the System R database manager. ACM Computing Surveys 13, 2 (1981), 223–242.

[17]

Gribble, S., Brewer, E., Hellerstein, J., and Culler, D. Scalable, distributed data structures for internet service construction. In Proc. of the 4th Symposium on Operating Systems Design and Implementation (Oct. 2004).

[18]

Haeberlen, A., Mislove, A., and Druschel, P. Glacier: Highly durable, decentralized storage despite massive correlated failures. In Proc. of the 2nd Symposium on Networked Systems Design and Implementation (May 2005).

[19]

Kleinrock, L. Queueing Systems, Volume I: Theory. John Wiley & Sons, Jan. 1975.

[20]

Kubiatowicz, J., Bindel, D., Chen, Y., Czerwinski, S., Eaton, P., Geels, D., Gummadi, R., Rhea, S., Weatherspoon, H., Weimer, W., Wells, C., and Zhao, B. OceanStore: An architecture for global-scale persistent storage. In Proc. of the 9th Intl. Conference on Architectural Support for Programming Languages and Operating Systems (Nov. 2000), pp. 190–201.

[21]

Lee, E. K., and Thekkath, C. A. Petal: Distributed virtual disks. In Proc. of the 7th Intl. Conference on Architectural Support for Programming Languages and Operating Systems (1996), pp. 84–92.

[22]

Leung, S.-T. A., MacCormick, J., Perl, S. E., and Zhang, L. Myriad: Cost-effective disaster tolerance. In Proc. of the 1st USENIX Conference on File and Storage Technologies (Jan. 2002).

[23]

Liskov, B., Ghemawat, S., Gruber, R., Johnson, P., Shrira, L., and Williams, M. Replication in the Harp file system. In Proc. of the 13th ACM Symposium on Operating System Principles (Oct. 1991), pp. 226–38.

[24]

Litwin, W., and Schwarz, T. LH* RS : A high-availability scalable distributed data structure using reed solomon codes. In Proc. of the 2000 ACM SIGMOD Intl. Conference on Management of Data (May 2000), pp. 237–248.

[25]

Park, K. S., and Pai, V. CoMon: a mostly-scalable monitoring system for PlanetLab. ACM SIGOPS Operating Systems Review 40, 1 (Jan. 2006), 65–74. https://comon.cs.princeton.edu/.

[26]

Patterson, D., Gibson, G., and Katz, R. A case for redundant arrays of inexpensive disks (RAID). In Proc. of the ACM SIGMOD International Conference on Management of Data (June 1988).

[27]

Patterson, H., Manley, S., Federwisch, M., Hitz, D., Kleiman, S., and Owara, S. Snapmirror: File system based asynchronous mirroring for disaster recovery. In Proc. of the 1st USENIX Conference on File and Storage Technologies (Jan. 2002).

[28]

Peterson, L., Anderson, T., Culler, D., and Roscoe, T. A blueprint for introducing disruptive technology into the Internet. In Proc. of the First ACM Workshop on Hot Topics in Networks (Oct. 2002). https://www.planet-lab.org.

[29]

Ramabhadran, S., and Pasquale, J. Analysis of long-running replicated systems. In Proc. of the 25th IEEE Annual Conference on Computer Communications (INFOCOM) (Apr. 2006).

[30]

Rhea, S., Eaton, P., Geels, D., Weatherspoon, H., Zhao, B., and Kubiatowicz, J. Pond: the OceanStore prototype. In Proc. of the 2nd USENIX Conference on File and Storage Technologies (Apr. 2003).

[31]

Rhea, S., Geels, D., Roscoe, T., and Kubiatowicz, J. Handling churn in a DHT. In Proc. of the 2004 Usenix Annual Technical Conference (June 2004).

[32]

Rodrigues, R., and Liskov, B. High availability in DHTs: Erasure coding vs. replication. In Proc. of the 4th International Workshop on Peer-to-Peer Systems (Feb. 2005).

[33]

Saito, Y., Froelund, S., Veitch, A., Merchant, A., and Spence, S. FAB: building distributed enterprise disk arrays from commodity components. In Proc. of the 11th Intl. Conference on Architectural Support for Programming Languages and Operating Systems (New York, NY, 2004), ACM Press, pp. 48–58.

[34]

Sit, E., Dabek, F., and Robertson, J. UsenetDHT: A low overhead Usenet server. In Proc. of the 3rd International Workshop on Peer-to-Peer Systems (Feb. 2004).

[35]

Stribling, J., Councill, I. G., Li, J., Kaashoek, M. F., Karger, D. R., Morris, R., and Shenker, S. OverCite: A cooperative digital research library. In Proc. of the 4th International Workshop on Peer-to-Peer Systems (Feb. 2005).

[36]

Stribling, J., Li, J., Councill, I. G., Kaashoek, M. F., and Morris, R. Exploring the design of multi-site web services using the OverCite digital library. In Proc. of the 3rd Symposium on Networked Systems Design and Implementation (May 2006).

[37]

Tati, K., and Voelker, G. M. On object maintenance in peer-to-peer systems. In Proc. of the 5th International Workshop on Peer-to-Peer Systems (Feb. 2006).

[38]

van Renesse, R., and Schneider, F. B. Chain replication for supporting high throughput and availability. In Proc. of the 6th Symposium on Operating Systems Design and Implementation (Dec. 2004).

[39]

Weatherspoon, H., Chun, B.-G., So, C. W., and Kubiatowicz, J. Long-term data maintenance in wide-area storage systems: A quantitative approach. Tech. Rep. UCB//CSD-05-1404, U. C. Berkeley, July 2005.

[40]

Weatherspoon, H., and Kubiatowicz, J. D. Erasure coding vs. replication: A quantitative comparison. In Proc. of the 1st International Workshop on Peer-to-Peer Systems (Mar. 2002).

This research was supported by the National Science Foundation under Cooperative Agreement No. ANI-0225660, https://project-iris.net/. Andreas Haeberlen was supported in part by the Max Planck Society. Emil Sit was supported in part by the Cambridge-MIT Institute. Hakim Weatherspoon was supported by an Intel Foundation PhD Fellowship.