
We introduce Scantegrity II, a practical enhancement for optical scan voting systems that achieves increased election integrity through the novel use of confirmation codes printed on ballots in invisible ink. Voters mark ballots just as in conventional optical scan but using a special pen that develops the invisible ink. Verifiability of election integrity is end-to-end, allowing voters to check that their votes are correctly included (without revealing their votes) and allowing anyone to check that the tally is computed correctly from the included votes. Unlike in the original Scantegrity, dispute resolution neither relies on paper chits nor requires election officials to recover particular ballot forms. Scantegrity II works with either precinct-based or central scan systems. The basic system has been implemented in open-source Java with off-the-shelf printing equipment and has been tested in a small election.
An enhancement to Scantegrity II keeps ballot identification and other unique information that is revealed to the voter in the booth from being learned by persons other than the voter. This modification achieves privacy that is essentially equivalent to that of ordinary paper ballot systems, allowing manual counting and recounting of ballots.
``Trust, but verify.''--Russian proverb, popularized by Ronald Reagan during his presidency
In order to provide increased confidence in the integrity of election outcomes, modern voting technology and legislation is moving from a model of trust to one that provides verifiability2 of some steps in the voting process. For example, with optical scan systems and voter-verified paper audit trails (VVPAT), voters can verify that their votes are correctly recorded on paper, and post-election manual recounts can verify that the paper trail matches the electronically produced tally. End-to-end (E2E) voting systems3 provide additional, stronger verifiability. E2E systems allow voters to verify that their ballots are processed correctly, giving voters assurance that their votes are cast, collected, and counted as intended. In essence, end-to-end voting systems provide a verifiable chain of custody on the ballots, from the start, when the votes are cast, to the end, when they are counted. They also enable the correctness of the final tally to be verified by anyone.
We propose Scantegrity II: Invisible Ink, an end-to-end security enhancement for existing optical scan voting systems that enables each voter to verify that her vote is processed correctly, without introducing any new polling place equipment. Extra information is printed on optical scan ballots during production, but the underlying method by which voters mark the ballots is not changed and remains in accordance with legislative proposals requiring ``unencrypted'' paper audit records. The E2E verifiability of Scantegrity II is opt-in; the voters who choose to ignore the additional features will have a voting experience similar to that with current optical scan. Additionally, Scantegrity II does not interfere with the security provisions of the underlying optical scan system: physical observation, validated tallying software, and recounts.
The basic Scantegrity II scheme, presented in Sections 3 through 6, provides the following new contributions.
The enhanced version of Scantegrity II, presented in Section 7, offers further contributions.
An end-to-end (E2E) approach to voting strives to provide verifiability of the integrity of key steps in the voting process. In particular, it allows verification that all cast ballots are included unmodified in the collection of ballots that are counted--a property assured by neither voter-verified paper audit trails (VVPAT) nor manual recounts. More formally, what have been variously called E2E, coded vote, cryptographic, or open-audit voting systems, are systems which preserve ballot secrecy while providing:
Cryptographic techniques were first applied to voting by Chaum [5], and Scantegrity II is a descendant of this paradigm [7,10,6]. An earlier paper-based system by Chaum [7] provides voter verifiability through a two-sheet ballot printed by a special printer that uses a transparent sheet and visual cryptography to show voter choices in a human-readable format. The voter destroys one sheet and keeps the other as a privacy-preserving receipt, a copy of which is publicly posted. It provides universal verifiability using a process similar to a mixnet [5] to decode the receipts and recover the plaintext ballots in an unlinkable manner.
The Punchscan [16,22] and Prêt à Voter [9] systems use simpler printing. In both systems, positional data from a printed ballot is publicly posted for voter verifiability. Each voter uses information printed on the unique ballot that indicates which positions correspond to which candidates in order to mark the ballot and subsequently destroys part of that information in order to hide her choices. To provide universal verifiability, the original Prêt à Voter uses a mixnet [5] and Punchscan uses a specialized anonymity network called the Punchboard, which combines tables of binding commitments [20,4] with randomized partial checking (RPC) [17]. It is now recognized, however, that such particular universal verifiability ``system back-ends'' can be mixed and matched with ``voter-facing front-ends.'' [19,24]
Both Punchscan and Prêt à Voter have numerous desirable security properties [25,14]. One potential issue, however, with any such system that publishes per-ballot contest results, including these two as well as Scantegrity, is known as the ``Italian attack'' or ``pattern voting.'' This has been solved for inter-contest patterns using so-called ``contest partitioning'' [23]. Another issue with these previous systems is so-called ``randomization attacks'' [15,18], in which a coercer can verify whether a voter has in effect randomized or biased the vote [18]. As mentioned earlier, these randomization attacks are solved by Scantegrity II.
The usability of the ballot marking process in any voting system can affect the accuracy of capturing voter intention. The indirect association of candidate order and mark order of the Punchscan ballot may conflict with the voter's mental model of how a ballot should be marked. On the other hand, voting systems requiring additional thought related to marking mechanics can increase the accuracy with which some voters mark. The experience of some of the authors using Punchscan in both mock and binding elections found no significant problems with the indirection [13].
In any case, Scantegrity [8] sidesteps these potential usability shortcomings by using a standard, non-randomized candidate ordering with adjacent bubbles, such as with conventional optical scan ballots. Each ballot independently associates a code with a particular candidate. The receipt therefore is simply a list of the codes of the selected candidates. This change interfaces directly with the pre-existing Punchscan anonymizing network [21], but election officials must recover individual paper ballots to settle disputes, and this leads to a cumbersome dispute resolution process in order to preserve voter privacy. The improvements presented in this paper eliminate the need for any such physical dispute resolution process.
The use of invisible ink is related to the concept of ballot casting assurance [1], where correctness of the receipt is verified by giving a voter a choice to audit it after it is created but before it is seen, proving to the voter that (with high probability) the receipt was generated correctly. This idea is also seen in Scratch & Vote [2] and Voter Initiated Auditing [3].
Scantegrity II is designed to meet several usability goals. Firstly and most importantly, the procedures for marking and casting a Scantegrity II ballot should deviate minimally from those of a conventional optical scan ballot. Secondly, the presence of a mechanism on the ballot for producing a receipt should not interfere with the marking and casting procedures. Finally, the procedures for producing and checking a receipt should be voluntary.
Here we present a high-level description of the voter experience for the basic system4:
A person who is eligible to vote is authenticated at the polling place in accordance with existing procedures governing voter registration. An authenticated voter is issued a single ballot for the purpose of voting and is given a decoder pen.
The voter enters the voting booth and uses the decoder pen to mark her choices on the ballot in the same manner as one would for a conventional optical scan ballot: a vote is indicated by marking a specially reserved region (referred to as a ``bubble'') directly beside the printed candidate/choice. The voter casts her ballot, again, in the same manner as one would for a conventional ``precinct'' optical scan ballot: a poll worker assists the voter in inputting the marked ballot into an optical scanner. The scanner reads the ballot ID and the states of the bubbles marked; it does not read the confirmation codes.
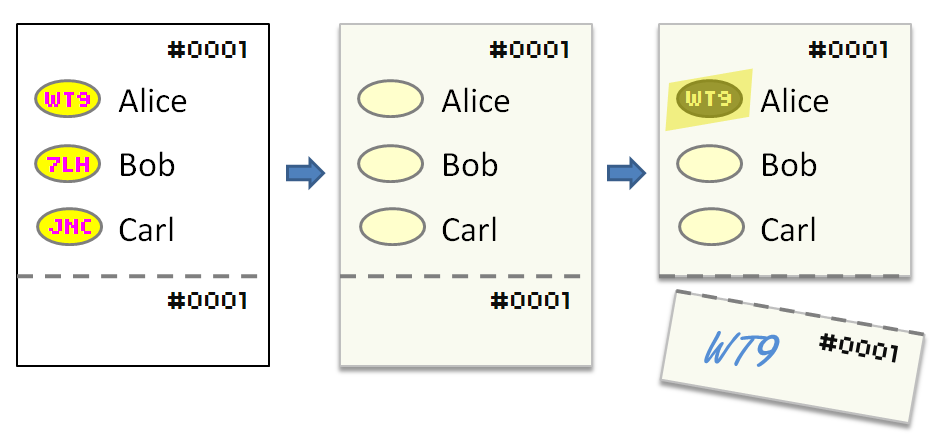
The voter can choose to participate in the voter verification process by creating a receipt of her vote. To create a receipt, the voter manually transcribes the revealed confirmation codes onto the receipt portion of her ballot. Afterwards, the receipt is indelibly marked as ``Ballot Voted'' by a poll worker (e.g., by a rubber stamp). The voter detaches the receipt from the ballot along a perforation and retains it for future reference. (It is preferable that receipts are detached for all ballots, whether or not the receipts are marked.)
In precinct-based optical scan environments, improperly marked ballots will be immediately rejected by the scanning device. If the local governing procedure allows the voter an additional attempt, the current ballot must first be invalidated before a new one is issued. The receipt (which includes the ballot ID) is detached and stamped as ``Spoiled Ballot'' and given to the voter. In order to protect voter privacy, the ballot itself should be destroyed in a verifiable manner (e.g., shredded).
During a previously announced time period after the conclusion of polling, the voter may check on the election website that election officials have correctly posted the revealed confirmation codes corresponding to her ballot ID. She may also check that her audit ballot is printed correctly (see Section 4.9). Also, any voter or interested party may check the correctness of the final tally posted on the election web site.
The receipt portion of the ballot contains space for the voter to optionally note the confirmation codes revealed by her selections. For convenience, the receipt portion may contain the list of contest titles with space next to each title for the voter to fill in the code. The receipt portion is located across the bottom of the ballot (so that its perforated edge does not interfere with scanner feeding) and is easily detachable by the voter along a perforation, as shown in Figure 1 (right).
Each ballot has a distinct ballot ID which uniquely identifies the election and the ballot within that election. An example ballot ID might be ``ST-2008-11-04-123456789.'' For simplicity, in the following examples we use 4-digit ballot IDs such as ``0001.'' The ballot ID is printed on both the voting portion and the receipt portion of the ballot. On the voting portion, the ballot ID may appear in the form of pre-filled bubbles for each character of the ID so that the optical scanner can read the ballot ID without using optical character recognition (OCR). Figure 1 (right) shows the ballot ID printed on the voting portion and the receipt portion of the ballot. (The pre-filled bubbles for the ballot ID are not shown.)
 |
![\begin{figure*}\centering\subtable[Table \textbf{P}]{
\begin{tabular}{\vert c\ve...
...hline & & \\
\hline & & \\
\hline & & \\
\hline
\end{tabular}}
\end{figure*}](img3.png) |
Because the Q- and S-pointers in table R are pseudorandomly generated, an element in table Q can map to any element of table R, which can map to any element of table S in the column for the corresponding candidate.
As a working example, consider an election with ![]() candidates, Alice, Bob, and Carl, and
candidates, Alice, Bob, and Carl, and ![]() ballots.
Figure 2 shows how the private tables
P, Q, R, and S generated by the
election officials might look before election day.
ballots.
Figure 2 shows how the private tables
P, Q, R, and S generated by the
election officials might look before election day.
A voter who is interested in verifying that her vote is collected as cast may transcribe the revealed confirmation codes onto the receipt portion of the ballot. The voter detaches the receipt portion of the ballot along a perforation.
As with conventional optical scan, the voter inserts her ballot into the optical scanner, which checks that the voter has not overvoted and that there are no stray marks. If there is an error, the scanner may reject the ballot and the voter can then either return to the booth to make additional marks or obtain a new ballot to vote on. Otherwise, the scanner accepts the ballot and records the voter's choices, along with the ballot ID.
After the voter casts her ballot, a poll worker stamps the voter's detached receipt as ``Ballot Voted''.
For each row of R, election officials open either the Q-pointer or the S-pointer, depending on a true random, publicly verifiable coin flip [11]. This information will be used to audit the election website via randomized partial checking (see Section 4.8).
For those ballots that were spoiled for audit, election officials open the commitments to all the information associated with the ballot, i.e., the confirmation codes in Q and the Q- and S-pointers in R.
Suppose ballots 0001 and 0003 are votes for Alice, ballot 0002 is a vote for Carl, ballot 0005 is a vote for Bob, and ballot 0004 is spoiled for audit (as described in Section 4.9). Figure 3 shows how the publicly published Q, R, and S tables would look at the end of election day.
![\begin{figure*}\centering\subtable[Table \textbf{Q}]{
\begin{tabular}{\vert c\ve...
...rk & & \checkmark\\
\hline \checkmark & &\\
\hline
\end{tabular}}\end{figure*}](img10.png) |
Disputes may arise under four general circumstances. They could be (i) the result of the voter making a transcription error, (ii) a mischievous voter attempting to call into question the legitimacy of the election, (iii) an error by the scanner or in the election data, or (iv) evidence of fraudulent behavior.
The election officials would like to distinguish the latter two cases from the former two, as the latter two cases undermine the integrity of the election and should trigger further investigation. Since voters do not see the confirmation codes of the unrevealed candidates on the ballot, the probability that a code that a voter claims to have revealed is one of the other codes committed to for her ballot is very small if the voter made a transcription error or is merely guessing. The election officials can publicly open the commitments to the other confirmation codes for the claimant's ballot and eliminate from consideration any disputes for which none of the opened codes matches the claimed code. We consider the remaining disputes to be ``plausible discrepancies.''
Plausible discrepancies could still be the product of cases (i) or (ii); however, the statistically expected number of them arising from random guessing is small and can be quantified. The election officials should set up a statistical trigger, based on various election parameters, such that if the number of plausible discrepancies exceeds some threshold, some suitable recourse is instigated.
Here we consider one possible statistical trigger. Consider a single
disputed race. Let ![]() be the number of candidates,
be the number of candidates, ![]() be the code space,
be the code space,
![]() be the number of disputes filed, and
be the number of disputes filed, and ![]() be number of plausible
discrepancies filed. Let
be number of plausible
discrepancies filed. Let ![]() be the probability of randomly guessing
a code that constitutes a plausible discrepancy. Then
be the probability of randomly guessing
a code that constitutes a plausible discrepancy. Then ![]() is the
expected value of
is the
expected value of ![]() if all filed disputes are random guesses. We
set the trigger
if all filed disputes are random guesses. We
set the trigger ![]() such that the probability of obtaining at least
such that the probability of obtaining at least ![]() plausible discrepancies if all filed disputes are random guesses is less than 1%.
We can use the following bound on the right tail of the binomial distribution [12]. For
any
plausible discrepancies if all filed disputes are random guesses is less than 1%.
We can use the following bound on the right tail of the binomial distribution [12]. For
any ![]() ,
,
![]() . For example, for
. For example, for ![]() candidates,
candidates, ![]() possible codes, and
possible codes, and ![]() disputes filed, assuming no scanning error,
disputes filed, assuming no scanning error,
![]() and
and
![]() . Using
. Using ![]() we get
we get
![]() , so we can set
, so we can set
![]() . If at least 5 out of the 1000 disputes filed are plausible
discrepancies, then an investigation should be instigated. To allow for up to some acceptable
rate
. If at least 5 out of the 1000 disputes filed are plausible
discrepancies, then an investigation should be instigated. To allow for up to some acceptable
rate ![]() of scanning error, we can incorporate
of scanning error, we can incorporate ![]() into the probability
into the probability ![]() of guessing a correct code
and compute the statistical trigger as above with the new value of
of guessing a correct code
and compute the statistical trigger as above with the new value of ![]() .
.
Any interested party can check that the commitments are correct, that each revealed Q-pointer in table R either connects a revealed code in table Q to a flagged element in table R or connects a hidden code to an unflagged element, and that each revealed S-pointer in table R either connects a flagged element in table R to a flagged element in table S or connects an unflagged element to an unflagged element. Essentially, the audit checks that flags are mapped unchanged from table Q through table R to table S.
Finally, any interested party can check that the tally for each candidate is correctly computed as the total number of flagged entries in that candidate's column in table S.
When a ballot is selected to be audited, a pollworker stamps the ballot as ``Audit Ballot'' on both the voting portion and the receipt portion and all of the confirmation codes on the ballot are revealed using a decoder pen. We will refer to the person checking an audited ballot as the auditor. The auditor checks that the confirmation codes are unique within each race. After election officials open the commitments to the confirmation codes in Q and the Q- and S-pointers for those confirmation codes, the auditor checks that the published confirmation codes match those revealed on the paper ballot, and that the published pointers map each confirmation code in Q to the appropriate candidate column in S.
Scantegrity II provides improved integrity properties over the underlying optical scan system and only minimally impacts the privacy and ballot secrecy properties. We provide a high-level sketch of several common attacks and the countermeasures Scantegrity II utilizes in thwarting them.
In our threat model, an adversary could be any party, including a voter, pollworker, or election official. The goal of the adversary is to attack the integrity of the election or exert undue influence over a voter. We do not consider attack vectors applicable to all voting systems, such as denial of service attacks, given that these attacks and countermeasures are not unique to Scantegrity II. Furthermore, we note that the security of Scantegrity II is equivalent in many regards to that of Punchscan and the original Scantegrity, for which security analyses are already present in academic literature [14,8]. We split our discussion of threats into those that affect integrity and those that affect privacy and ballot secrecy.
Integrity of an election refers to the inability of an adversary to modify votes undetectably. Compared to conventional optical scan, Scantegrity II provides improved ability to detect an attacker attempting to affect the integrity of an election by modifying ballots, creating fraudulent ballots, or attempting to change the tally on the election website.
An adversary might attempt to delete ballots from the bulletin board by marking voted ballots as spoiled for audit and publishing all of the information associated with those ballots. Then he runs the risk of the voters of those ballots checking the election website and protesting that their ballots were incorrectly posted as spoiled for audit, providing their stamped receipts as proof.
If an adversary adds more marks to a ballot after it has been cast, it can be detected by public observation of the election website if the additional marks turned a valid ballot into an overvoted one. Some optical scan systems prevent this attack because they do not accept overvoted ballots, but the adversary could add a mark to a ballot which was originally an undervote. This can be detected by the voter of that ballot, but the voter has no proof that the mark was added later. One way to address this is to always include a ``None of the above" option on each race, which voters could optionally mark to submit an undervote.
There are several types of fraudulent ballots that the election officials could create or that an adversary could substitute for properly constructed ballots:
In all of these cases, the fraudulent ballots can be detected by the cut-and-choose auditing of the ballots. If a random half of the ballots are audited, no more than a few fraudulent ballots should go undetected.
More precisely, if there are ![]() total ballots,
total ballots, ![]() fraudulent
ballots, and
fraudulent
ballots, and ![]() ballots are audited, then the probability that the
adversary will go undetected is
ballots are audited, then the probability that the
adversary will go undetected is
![]() ,
which can be straightforwardly shown to be upper bounded by
,
which can be straightforwardly shown to be upper bounded by
![]() .
.
An adversary may try to change the vote tally by flipping flags in
Q, R, or S, so that counting the flags
for each candidate in table S gives an incorrect tally.
This can be detected by the randomized partial checking of the
Q- and S-pointers in R. The probability
of an adversary modifying ![]() pointers going undetected is
pointers going undetected is ![]() .
.
Privacy refers to the inability of an attacker to link a voter's candidate choices to the voter. Modeling privacy in a voting system requires strong assumptions due to the wide variety of physical attacks that could violate voter privacy in any voting system. Given our assumptions, Scantegrity II offers the same privacy protection as for conventional optical scan systems. However, privacy concerns arise if these assumptions are relaxed. The enhancements presented in Section 7 address these privacy concerns.
If the generation of the confirmation codes or the secrecy of the private information in the tables is compromised, an adversary could violate a voter's privacy. If an adversary obtains access to cast ballot forms and obtains the ballot ID used by a voter, he will be able to determine that voter's choices. To address these threats, we make the assumptions that no recording devices are present in the polling booth and chain-of-custody procedures are enforced to ensure that an adversary does not have access to the ballot boxes. Further countermeasures are possible, for example, ensuring that the ballot ID on the cast portion of the ballots is difficult to extract. One possibility is to encrypt the ballot ID or make it not human-readable.
Both the ballot and confirmation codes are printed before voting takes place. Three types of inks are employed for this purpose. Conventional (e.g., black) ink is used for primary printing of candidate names, instructions, other text, etc. For the purposes of printing confirmation codes, two specialty inks are employed: a reactive invisible ink and an non-reactive color-matched dummy ink.
The term ``invisible ink'' refers to an ink with the following properties:
However, the term ``invisible ink'' is a misnomer in the sense that any liquid (though not necessarily pigmented) will subtly change the reflective characteristics of the print medium through the printing process, meaning the presence of letters printed in invisible ink also will still potentially be visually perceptible. For this reason we employ a dummy ink with the following properties:
We define a matrix of pixels for the purposes of printing the confirmation codes inside the optical scan bubbles. Pixels that form the ``foreground'' confirmation code characters are printed in one ink, while the remaining ``background'' pixels are printed in the other ink. In order to produce the darkest average color density of a marked optical scan bubble (and therefore most visible to the scanner), the background pixels are printed with the invisible ink, and the foreground pixels are printed in the non-reactive dummy ink. Therefore when marked by the decoder pen, the bubble will contain lightly pigmented letters against a dark background.
The developer ink is incorporated into a felt-tipped ``highlighter'' style marker along with a basic yellow pigment to provide voters with visual feedback as to where they have marked. We have implemented the invisible ink printing process using an Epson C88+ color inkjet printer in which we replace the manufacturer-supplied yellow and magenta inks with the reactive and non-reactive inks respectively. Electronic files used for ballot printing are prepared in this false-color mapping whereby yellow and magenta colored regions in the digital file will print in reactive and non-reactive inks respectively. This process is depicted in Figure 4.
In this section, we suggest ways to improve the basic Scantegrity II system described thus far. One enhancement allows all information on the ballot to be humanly-visible only within a short window of time. Another improvement allows information seen by the voter to be sufficient for the voter to complain, thereby reducing the efficacy of attacks in which physical receipt may be obtained from voters.
In the basic system, uniquely identifiable codes are left on the paper ballots at the conclusion of the election, making manual recounts potentially useful in improper influence schemes, such as vote buying and coercion. Even though manual recounts are a weaker integrity guarantee than that offered by the Scantegrity II audit, it is preferable to be able to allow both. Our first enhancement, designed to permit recounts, utilizes a ``slow-reacting'' invisible ink--created by diluting the concentration of the reactants in the normal invisible ink or introducing a chemical inhibitor. When brought into contact with the developer ink, this ink has a much lower reaction rate--on the order of tens of minutes instead of fractions of a second. By replacing the dummy ink on the foreground pixels of each confirmation code on a ballot with slow-reacting ink, a bubble undergoes an immediate reaction upon marking, making the codes visible to the voter. A slow reaction will, however, gradually (e.g., over 15 minutes) begin to fade the foreground pixels of the confirmation code to an indistinguishable color, filling in the bubble completely and hiding the confirmation code. The ballots can then be re-scanned and/or manually counted or recounted, as often as desired, without revealing confirmation codes to the persons involved.
When a ballot is audited, the confirmation codes can be revealed using one of the decoder pens used for voting (to audit the effectiveness of the pen) or taken home by the voter and developed if she has access to the ink. To prevent the confirmation codes from fading, the voter can choose to apply a fixative, by spraying or sponging her ballot, that completely inhibits the slow-reacting ink and preserves the codes.
Disputes in the basic system require physical possession of a stamped receipt. The second enhancement allows for informational disputes, where a voter need only know her confirmation codes in order to prove that her ballot is misrepresented online. Further, to prevent the threat of voted ballots being turned into audited or spoiled ballots without stamped receipts, two additional ``authenticated ballot status'' codes are added to the ballot. These status codes are the same size as the confirmation codes, are committed to prior to the election, printed on the ballot in slow-reacting ink, and are individually detachable (e.g., using a perforation). If a ballot is chosen for a print audit by the voter, one of these codes is developed by the poll worker and the other detached and destroyed--which one is the choice of the voter. If a ballot is chosen to be voted on, both codes are retained on the ballot, detached prior to feeding the ballot into the optical scanner, and developed by the poll worker after the ballot is successfully cast. Within a few minutes, the voter is able to read the codes. If the ballot is spoiled (e.g., the voter overvoted and is issued another ballot), the chit is returned by the voter and checked as matching the ballot being spoiled and then both codes are shredded without being developed. If a voter later finds that her cast ballot has been misrepresented as an audited or spoiled ballot on the website, knowledge of both of the codes is necessary and sufficient for proving the ballot was voted, indicating malfeasance or error. Similarly, if a voter discovers that her audited vote has been misrepresented as a voted or spoiled ballot, knowledge of one code is sufficient to prove that the ballot was not spoiled and knowledge of all the confirmation codes is sufficient to prove that the ballot was not voted on.5 In order to dispute an incorrect confirmation code that appears online, the voter need only know a proper code and does not need to actually have the physical receipt (stamped or otherwise). Given that voters are provided adequate time in the booth to memorize or copy the codes, obtaining a voter's stamped receipt after the election is not sufficient to prevent the voter from detecting an error on the election website and filing a successful dispute.
Since no physical evidence is required for a dispute, the dispute resolution process does not have to occur in person and the voter can file an online petition instead (optionally anonymously). This may be advantageous in situations where the voter has reason to fear retribution for reporting errors. To prevent the system from being what may be called ``flooded'' with spurious complaints, sensible precautions can be taken to eliminate blatantly fraudulent claims, including CAPTCHAs and limits on complaints per IP address. If dispute flooding occurs, however, the resolution can move to a second phase where candidates or political parties are allocated a fixed number of complaints per flooded ballot and can then choose the most plausible complaints as they prefer.
These improvements do not interfere with Scantegrity II's ability to be used in central-scan environments. As the scanner does not need to record the confirmation codes, since the positions marked are sufficient to reconstruct the codes, ballots may be scanned after the slow-reacting ink has hidden the confirmation codes. This is useful for precincts that lack scanning equipment, as is the case in many developing democracies. Scantegrity II can also augment hand-counted elections by allowing the ballot-counting to proceed as usual, and then providing the ability for the ballots to be centrally scanned after the election to ensure end-to-end integrity.
Scantegrity II provides voters with a familiar optical scan voting experience as well as an option to verify that their ballots ``make it, as intended, all the way.'' This end-to-end verification capability enables election officials to provide the highest level of assurance that outcomes are correct and in a way that is visible to voters. The system also improves on its predecessor by removing the need to recover paper ballots in resolving disputes about the information posted on the election website and allows for manual recount.
While further testing and development are planned, Scantegrity II holds promise of being the first end-to-end voting system to come into use in public sector elections.
We are grateful to Russell Fink for reviewing several versions of the paper, and the Ottawa Canada Linux Users Group for test-driving our system and providing useful feedback.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation ScantegrityII.tex
The translation was initiated by Emily H. Shen on 2008-07-01